题目内容
7.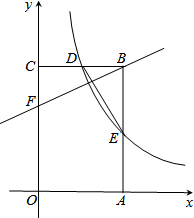 如图,矩形OABC的顶点A、C分别在x轴和y轴上,点B的坐标为(2,3),双曲线y=$\frac{k}{x}$(x>0),的图象经过BC上的点D与AB交于点E,连接DE,若若E是AB的中点﹒
如图,矩形OABC的顶点A、C分别在x轴和y轴上,点B的坐标为(2,3),双曲线y=$\frac{k}{x}$(x>0),的图象经过BC上的点D与AB交于点E,连接DE,若若E是AB的中点﹒(1)求D点的坐标;
(2)点F是OC边上一点,若△FBC和△DEB相似,求BF的解析式;
(3)若点P(m,3m+6)也在此反比例函数的图象上(其中m>0),过P点作x轴的垂线,交x轴于点M,若线段PM上存在一点Q,使得△OQM的面积是$\frac{1}{2}$,设Q点的纵坐标为n,求n2-2n+9的值.
分析 (1)先求出点E的坐标,求出双曲线的解析式,再求出CD=1,即可得出点D的坐标;
(2)分两种情况:①△FBC和△DEB相似,当BD和BC是对应边时,$\frac{BD}{BE}=\frac{BC}{CF}$,求出CF,得出F的坐标,用待定系数法即可求出直线BF的解析式;
②当BD与CF是对应边时,$\frac{BD}{BE}=\frac{CF}{BC}$,求出CF、OF,得出F的坐标,用待定系数法即可求出直线BF的解析式;
(3)由题意得出m(3m+6 )=3,即m2+2m-1=0,由三角形的面积得出m•n=1,代入得出n2-2n=1,即可得出所求式子的值.
解答 解:(1)∵四边形ABCD是矩形,
∴OA=BC,AB=OC,
∵B(2,3),E为AB的中点,
∴AB=OC=3,OA=BC=2,AE=BE=$\frac{1}{2}$AB=$\frac{3}{2}$,
∴E(2,$\frac{3}{2}$),
∴k=2×$\frac{3}{2}$=3,
∴双曲线解析式为:y=$\frac{3}{x}$;
∵点D在双曲线y=$\frac{3}{x}$(x>0)上,
∴OC•CD=3,
∴CD=1,
∴点D的坐标为:(1,3);
(2)∵BC=2,CD=1,
∴BD=1,
分两种情况:
①△FBC和△DEB相似,当BD和BC是对应边时,$\frac{BD}{BE}=\frac{BC}{CF}$,
即$\frac{1}{\frac{3}{2}}=\frac{2}{CF}$,
∴CF=3,
∴F(0,0),
即F与O重合,
设直线BF的解析式为:y=kx,
把点B(2,3)代入得:k=$\frac{3}{2}$,
∴直线BF的解析式为:y=$\frac{3}{2}$x;
②△FBC和△DEB相似,当BD与CF是对应边时,$\frac{BD}{BE}=\frac{CF}{BC}$,
即$\frac{1}{\frac{3}{2}}=\frac{CF}{2}$,
∴CF=$\frac{4}{3}$,
∴OF=3-$\frac{4}{3}$=$\frac{5}{3}$,
∴F(0,$\frac{5}{3}$),
设直线BF的解析式为:y=ax+c,
把B(2,3),F(0,$\frac{5}{3}$)代入得:$\left\{\begin{array}{l}{2a+c=3}\\{c=\frac{5}{3}}\end{array}\right.$,
解得:a=$\frac{2}{3}$,c=$\frac{5}{3}$,
∴直线BF的解析式为:y=$\frac{2}{3}$x+$\frac{5}{3}$;
综上所述:若△FBC和△DEB相似,BF的解析式为:y=$\frac{3}{2}$x,或y=$\frac{2}{3}$x+$\frac{5}{3}$;
(3)∵点P(m,3m+6)在反比例函数y=$\frac{3}{x}$的图象上,
∴m(3m+6 )=3,
整理得:m2+2m-1=0,
∵PQ⊥x轴,
∴Q点的坐标为:(m,n)
∵△OQM的面积为$\frac{1}{2}$,
∴$\frac{1}{2}$OM•QM=$\frac{1}{2}$,
∴OM•QM=1,
∵m>0,
∴m•n=1
∴m=$\frac{1}{n}$,
代入m2+2m-1=0得:$\frac{1}{{n}^{2}}+\frac{2}{n}$-1=0,
即n2-2n-1=0,
∴n2-2n=1,
∴n2-2n+9=10.
点评 本题是反比例函数综合题目,考查了矩形的性质、坐标与图形性质、相似三角形的性质、用待定系数法求反比例函数和一次函数的解析式、三角形面积的计算等知识;本题难度较大,综合性强,特别是(2)中,需要进行分类讨论,运用相似三角形的性质求出点的坐标才能得出结果.

| A. | 一元硬币的直径 | B. | 数学课本宽度 | ||
| C. | 五层楼房的高度 | D. | 初中学生小丽的身高 |
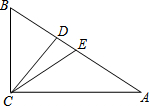 在直角三角形ABC中,CD、CE分别是斜边AB上的高、中线,BC=a,AC=b
在直角三角形ABC中,CD、CE分别是斜边AB上的高、中线,BC=a,AC=b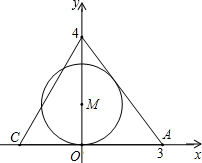 如图,直角坐标系中,点A(3,0)、B(0,4)分别位于x轴和y轴上,点C在x轴的负半轴上,且∠ACB=60°,在y轴正半轴上有一点M,以M为圆心,MO为半径作⊙M与BA相切,若保持圆的大小不变,△ABC位置不变,将⊙M向右平移$\frac{\sqrt{3}}{6}$个单位,⊙M与BC相切.
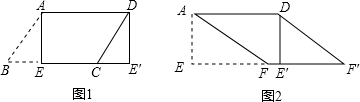
如图,直角坐标系中,点A(3,0)、B(0,4)分别位于x轴和y轴上,点C在x轴的负半轴上,且∠ACB=60°,在y轴正半轴上有一点M,以M为圆心,MO为半径作⊙M与BA相切,若保持圆的大小不变,△ABC位置不变,将⊙M向右平移$\frac{\sqrt{3}}{6}$个单位,⊙M与BC相切.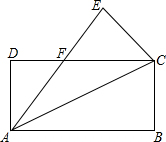 根据要求将下面题目改编成一道新题:如图,将矩形ABCD沿对角线AC折叠,点B落在E处,AE交DC于点F,求证:折叠后的重叠部分(即△FAC)是等腰三角形
根据要求将下面题目改编成一道新题:如图,将矩形ABCD沿对角线AC折叠,点B落在E处,AE交DC于点F,求证:折叠后的重叠部分(即△FAC)是等腰三角形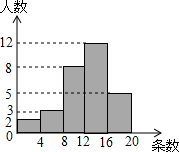 某项针对18岁~35岁的青年人每天发微博数量的调查中,随机对30名符合年龄的青年人开展每人“日均发微博条数”的调查,并绘制成如图所示的频数分布直方图,请根据频数分布直方图估计这30名青年人中“日均发微博条数”的平均数.
某项针对18岁~35岁的青年人每天发微博数量的调查中,随机对30名符合年龄的青年人开展每人“日均发微博条数”的调查,并绘制成如图所示的频数分布直方图,请根据频数分布直方图估计这30名青年人中“日均发微博条数”的平均数.