题目内容
△ABC是等腰直角三角形，BD平分∠ABC，CE⊥BD于E，交BA的延长线于F，
（1）求证：EF=EC；
（2）求证：BD=2EC．
证明：（1）∵∠1=∠2，∠BEF=∠BEC=90°，BE=BE，
∴△BEF≌△BEC，
∴EF=FC；
（2）∠1+∠BDA=90°，∠3+∠CDE=90°，
∴∠1=∠3，
又BA=CA，∠BAD=∠CAF，
∴△BAD≌△CAF，
∴BD=CF=2EC．
分析：（1）根据已知利用AAS判定△BEF≌△BEC，从而得到BF=BC．
（2）先证∠1=∠3，然后可证得△BAD≌△CAF，从而可得出答案．
点评：本题考查等腰直角三角形的性质，难度不大，注意利用全等三角形的性质证线段的相等．
∴△BEF≌△BEC，
∴EF=FC；
（2）∠1+∠BDA=90°，∠3+∠CDE=90°，
∴∠1=∠3，
又BA=CA，∠BAD=∠CAF，
∴△BAD≌△CAF，
∴BD=CF=2EC．
分析：（1）根据已知利用AAS判定△BEF≌△BEC，从而得到BF=BC．
（2）先证∠1=∠3，然后可证得△BAD≌△CAF，从而可得出答案．
点评：本题考查等腰直角三角形的性质，难度不大，注意利用全等三角形的性质证线段的相等．
练习册系列答案
阅读快车系列答案
相关题目
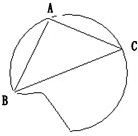如图，要把破残的圆形模具复制完整，已知弧上的三点A、B、C；
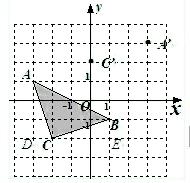16、如图，在画有方格图的平面直角坐标系中，△ABC的三个顶点均在格点上．
在△ABC中，∠ACB=90°，点A的坐标为（0，2），点B（-3，1）在抛物线y=ax2+ax-2上，点C在x轴上．