题目内容
如图①,△ABC中, ,∠ABC=
,∠ABC= ,将△ABC绕点A顺时针旋转得到△AB ¢C ¢,设旋转的角度是
,将△ABC绕点A顺时针旋转得到△AB ¢C ¢,设旋转的角度是 .
.


(1)如图②,当
 =" " °(用含
=" " °(用含 的代数式表示)时,点B ¢恰好落在CA的延长线上;
的代数式表示)时,点B ¢恰好落在CA的延长线上;(2)如图③,连结BB ¢、CC ¢, CC ¢的延长线交斜边AB于点E,交BB ¢于点F.请写出图中两对相似三角形 ,
(不含全等三角形),并选一对证明.
(1)

(2)略解析:
解:(1)
 ……………………………………………………………1分
……………………………………………………………1分(2)图中两对相似三角形:①△ABB ¢∽△AC C ¢,②△ACE∽△FBE;……… 3分
证明①:∵△ABC绕点A顺时针旋转角
 得到△AB ¢C ¢
得到△AB ¢C ¢∴∠CA C ¢=∠BAB ¢=
 ,AC="A" C ¢,AB="AB" ¢ ………………………………4分
,AC="A" C ¢,AB="AB" ¢ ………………………………4分∴
 ……………………………………………………5分
……………………………………………………5分∴△ABB ¢∽△AC C ¢ ……………………………………………………6分
证明②:∵△ABC绕点A顺时针旋转角
 得到△AB ¢C ¢
得到△AB ¢C ¢∴∠CA C ¢=∠BAB ¢=
 ,AC="A" C ¢,AB="AB" ¢ ………………………………4分
,AC="A" C ¢,AB="AB" ¢ ………………………………4分∴∠AC C ¢=∠ABB ¢=
 ………………………………5分
………………………………5分 又∠A E C =∠FEB
∴△ACE∽△FBE ……………………………………………………6分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
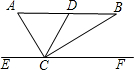 如图,Rt△ABC中,DC是斜边AB上的中线,EF过点C且平行于AB.若∠BCF=35°,则∠ACD的度数是( )
如图,Rt△ABC中,DC是斜边AB上的中线,EF过点C且平行于AB.若∠BCF=35°,则∠ACD的度数是( )| A、35° | B、45° | C、55° | D、65° |
 17、如图,在△ABC中,AB=AC,AD是△ABC的平分线,DE⊥AB,DF⊥AC,垂足分别是E,F.则下面结论中①DA平分∠EDF;②AE=AF,DE=DF;③AD上的点到B、C两点距离相等;④图中共有3对全等三角形,正确的有:
17、如图,在△ABC中,AB=AC,AD是△ABC的平分线,DE⊥AB,DF⊥AC,垂足分别是E,F.则下面结论中①DA平分∠EDF;②AE=AF,DE=DF;③AD上的点到B、C两点距离相等;④图中共有3对全等三角形,正确的有: 8、如图,在△ABC中,AB=20cm,AC=12cm,点P从点B出发以每秒3cm的速度向点A运动,点Q从点A同时出发以每秒2cm的速度向点C运动,其中一个动点到达端点时,另一个动点也随之停止运动,当△APQ是等腰三角形时,运动的时间是( )
8、如图,在△ABC中,AB=20cm,AC=12cm,点P从点B出发以每秒3cm的速度向点A运动,点Q从点A同时出发以每秒2cm的速度向点C运动,其中一个动点到达端点时,另一个动点也随之停止运动,当△APQ是等腰三角形时,运动的时间是( )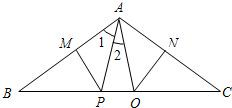 如图,在△ABC中,AB=AC,∠BAC=100°,MP、NO分别垂直平分AB、AC,求∠1,∠2的度数.
如图,在△ABC中,AB=AC,∠BAC=100°,MP、NO分别垂直平分AB、AC,求∠1,∠2的度数. 19、如图,在△ABC中,∠C=90°,DE⊥AB于E,DF⊥BC于F.求证:△DEH∽△BCA.
19、如图,在△ABC中,∠C=90°,DE⊥AB于E,DF⊥BC于F.求证:△DEH∽△BCA.