题目内容
如图折叠直角三角形纸片的直角，使点C落在斜边AB上的点E处．已知AB=
，∠B=30°，则DE的长是________．
4
分析：根据折叠得到∠EAD=∠B=30°，AE=BE=4
，再结合30°直角三角形的性质和勾股定理即可求得DE的长．
解答：根据题意，得∠EAD=∠B=30°，AE=BE=4．
设DE=x，则AD=2x，根据勾股定理，得
x2+48=4x2，
解得x=4．
∴DE=4．
故答案为：4．
点评：此题考查了翻折变化和角平分线的性质，对于折叠问题找准相等关系，得AD平分∠BAC是解题的关键．
分析：根据折叠得到∠EAD=∠B=30°，AE=BE=4
，再结合30°直角三角形的性质和勾股定理即可求得DE的长．解答：根据题意，得∠EAD=∠B=30°，AE=BE=4
．设DE=x，则AD=2x，根据勾股定理，得
x2+48=4x2，
解得x=4．
∴DE=4．
故答案为：4．
点评：此题考查了翻折变化和角平分线的性质，对于折叠问题找准相等关系，得AD平分∠BAC是解题的关键．
练习册系列答案
相关题目
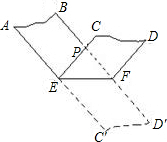
25、在折纸游戏中，将一条两边沿互相平行的纸带如图折叠，小明在游戏中发现：不管折叠角度∠CPB是锐角、直角或钝角，△PEF始终是等腰三角形．你认为他的想法对吗？请说明理由．
在折纸游戏中，将一条两边沿互相平行的纸带如图折叠，小明在游戏中发现：不管折叠角度∠CPB是锐角、直角或钝角，△PEF始终是等腰三角形．你认为他的想法对吗？请说明理由．