题目内容
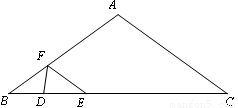
如图，在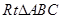
中，
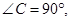以AC为直径作⊙O，交AB边于点D，过点O作OE∥AB，交BC边于点E.
（1）试判断ED与⊙O位置关系，并给出证明；
（2）如果⊙O的半径为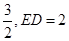
，求AB的长.
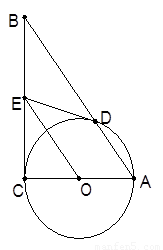
【答案】
解：（1）连结OD，
∵OD=0C,∠DOE=COE,OE=OE
∴
，
得 
即ED与
相切。
（2）DE=2,由，得CE=2,由OE∥AB，O为AC的中点，
得BC=4
R=3/2,AC=3
【解析】（1）连接OD，则，所以根据切线的判定定理即可得到DE与⊙O相切；
（2）在直角三角形ACB中，求得BC的长，即可用勾股定理得出斜边AB的长。
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，△ABC中，以BC为边向外作△BCD，把△ABD绕着点D按顺时针方向旋转60°得到△ECD的位置，A、C、E三点恰好在同一直线上．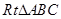
中，
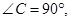以AC为直径作⊙O，交AB边于点D，过点O作OE∥AB，交BC边于点E.
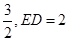，求AB的长.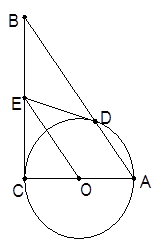 
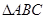中，AB=AC，以AB为直径的
交BC于点M，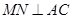
于点N.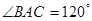
，AB=2，求图中阴影部分的面积.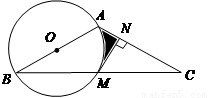
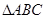中，AB=AC=10cm，
BC=16cm，DE=4cm．线段DE（端点D从点B开始）沿BC边以1cm／s的速度向点C运动，当端点E到达点C时停止运动．过点E作EF∥AC交AB于点F，连接DF，设运动的时间为t秒（t≥0）．