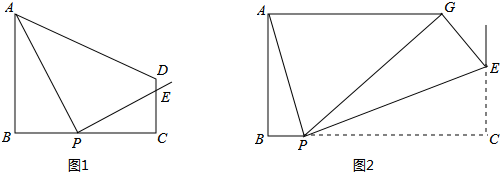题目内容
 设P、Q为线段BC上两定点,且BP=CQ,A为BC外一动点,如图,当A运动到使∠BAP=∠CAQ时,△ABC的形状是________.
设P、Q为线段BC上两定点,且BP=CQ,A为BC外一动点,如图,当A运动到使∠BAP=∠CAQ时,△ABC的形状是________.
等腰三角形
分析:假设AB≠AC,不妨设AB>AC,则∠B<∠C,故∠QPA<∠AQP,则AP>AQ.然后在△ABQ、△ACQ中分别应用正弦定理求得AP•AB=AC•AQ;又有AB>AC推知AP<AQ,这与AP>AQ矛盾,所以假设不成立,故而AB=AC,所以该三角形是等腰三角形.
解答:反证法.
假设AB≠AC,不妨设AB>AC,则∠B<∠C,故∠QPA<∠AQP,则AP>AQ,
在△ABQ、△ACQ中分别应用正弦定理,得
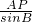 =
=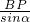 =
=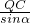 =
=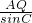 ,
,
则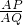 =
=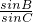 =
= ,
,
∴AP•AB=AC•AQ
又∵AB>AC,
∴AP<AQ,这与AQ>AQ矛盾,
∴AB=AC,从而△ABC为等腰三角形.
故答案为:等腰三角形.
点评:本题综合考查了等腰三角形的判定、正弦定理与余弦定理.解答此题时,采用了“反证法”.
分析:假设AB≠AC,不妨设AB>AC,则∠B<∠C,故∠QPA<∠AQP,则AP>AQ.然后在△ABQ、△ACQ中分别应用正弦定理求得AP•AB=AC•AQ;又有AB>AC推知AP<AQ,这与AP>AQ矛盾,所以假设不成立,故而AB=AC,所以该三角形是等腰三角形.
解答:反证法.
假设AB≠AC,不妨设AB>AC,则∠B<∠C,故∠QPA<∠AQP,则AP>AQ,
在△ABQ、△ACQ中分别应用正弦定理,得
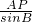 =
=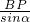 =
=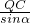 =
=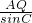 ,
,则
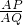 =
=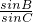 =
= ,
,∴AP•AB=AC•AQ
又∵AB>AC,
∴AP<AQ,这与AQ>AQ矛盾,
∴AB=AC,从而△ABC为等腰三角形.
故答案为:等腰三角形.
点评:本题综合考查了等腰三角形的判定、正弦定理与余弦定理.解答此题时,采用了“反证法”.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
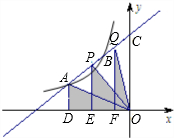 如图,直线l交y轴于点C,与双曲线y=
如图,直线l交y轴于点C,与双曲线y=| k |
| x |
| A、S1<S2<S3 |
| B、S3<S1<S2 |
| C、S3<S2<S1 |
| D、S1、S2、S3的大小关系无法确定 |
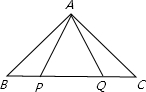 1、设P、Q为线段BC上两点,且BP=CQ,A为BC外一动点(如图).当点A运动到使∠BAP=∠CAQ时,△ABC是什么三角形?试证明你的结论.
1、设P、Q为线段BC上两点,且BP=CQ,A为BC外一动点(如图).当点A运动到使∠BAP=∠CAQ时,△ABC是什么三角形?试证明你的结论.