题目内容
 已知直线l1:y=3x+1与y轴交于点A,与x交于点C,直线l2:y=mx+n交于点P(-2,a),l1过第一、二、三象限; l2过第一、三、四象限,
已知直线l1:y=3x+1与y轴交于点A,与x交于点C,直线l2:y=mx+n交于点P(-2,a),l1过第一、二、三象限; l2过第一、三、四象限,(1)求3x+1>mx的解集;
(2)当x=3时,直线l2表示的一次函数值恰好等于零,求直线l2的函数解析式;
(3)若直线l1上有一点D,使S△BCD=S△BCP,求点D的坐标;
(4)在x轴上找一点E,使△ABE是等腰三角形,求出点E的坐标.
考点:一次函数综合题
专题:
分析:(1)根据图示直接回答问题;
(2)把点P的坐标代入直线l1后求得a的值;然后把点P和(3,0)分别代入直线l2,联立方程组来求m、n的值;
(3)根据等式可以判定点D到x轴的距离等于点P到x轴的距离;
(4)需要分类讨论:AB=AE、AE=BE、AB=BE.
(2)把点P的坐标代入直线l1后求得a的值;然后把点P和(3,0)分别代入直线l2,联立方程组来求m、n的值;
(3)根据等式可以判定点D到x轴的距离等于点P到x轴的距离;
(4)需要分类讨论:AB=AE、AE=BE、AB=BE.
解答: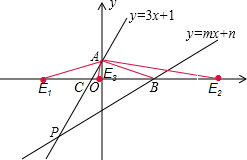 解:(1)如图,∵直线l1与直线l2交于点P(-2,a),
解:(1)如图,∵直线l1与直线l2交于点P(-2,a),
∴3x+1>mx的解集是x>-2;
(2)∵点P(-2,a)在直线y=3x+1上,
∴a=3×(-2)+1=-5,则P(-2,-5).
又∵当x=3时,直线l2表示的一次函数值恰好等于零,点P在直线直线y=mx+n上,
∴
,
解得
,
故直线l2的函数解析式是y=3x-3;
(3)∵S△BCD=S△BCP,且点D在直线l1上,P(-2,-5).
∴点D到x轴的距离与点P到x轴的距离相等,
∴设D(t,5),
则5=3t+1,
解得 t=
.
故点D的坐标是(
,5);
(4)由直线y=3x+1和直线y=3x-3易求得:A(0,1),B(1,0).
则AB=
.
当△ABE是等腰三角形时,需要分三种情况进行讨论:
①当AB=AE时,点A在BE的垂直平分线上,则点B与点E关于y轴对称,故点E1的坐标为(-1,0);
②当AB=BE时,故E2(1+
,0),E3=(
-1,0);
③当AE=BE时,点E与原点O重合,则E4(0,0).
综上所述,符合条件的点E的坐标有4个:(-1,0)、(1+
,0)、(
-1,0)或(0,0).
 解:(1)如图,∵直线l1与直线l2交于点P(-2,a),
解:(1)如图,∵直线l1与直线l2交于点P(-2,a),∴3x+1>mx的解集是x>-2;
(2)∵点P(-2,a)在直线y=3x+1上,
∴a=3×(-2)+1=-5,则P(-2,-5).
又∵当x=3时,直线l2表示的一次函数值恰好等于零,点P在直线直线y=mx+n上,
∴
|
解得
|
故直线l2的函数解析式是y=3x-3;
(3)∵S△BCD=S△BCP,且点D在直线l1上,P(-2,-5).
∴点D到x轴的距离与点P到x轴的距离相等,
∴设D(t,5),
则5=3t+1,
解得 t=
| 4 |
| 3 |
故点D的坐标是(
| 4 |
| 3 |
(4)由直线y=3x+1和直线y=3x-3易求得:A(0,1),B(1,0).
则AB=
| 2 |
当△ABE是等腰三角形时,需要分三种情况进行讨论:
①当AB=AE时,点A在BE的垂直平分线上,则点B与点E关于y轴对称,故点E1的坐标为(-1,0);
②当AB=BE时,故E2(1+
| 2 |
| 2 |
③当AE=BE时,点E与原点O重合,则E4(0,0).
综上所述,符合条件的点E的坐标有4个:(-1,0)、(1+
| 2 |
| 2 |
点评:本题综合考查了待定系数法求一次函数的解析式、一次函数交点问题以及等腰三角形的判定与性质.解答(4)题时,一定要分类讨论,以防漏解.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
方程xy-x-y-2=0的整数解的个数为( )
| A、1 | B、2 | C、3 | D、4 |
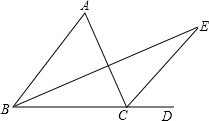 如图,在△ABC中,D是BC延长线上的一点,∠ABC,∠ACD的角平分线交于点E.求证:∠E=
如图,在△ABC中,D是BC延长线上的一点,∠ABC,∠ACD的角平分线交于点E.求证:∠E=