题目内容
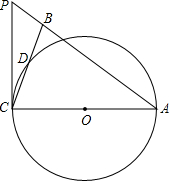 如图,在△ABC中,以AC为直径的⊙O交BC于D,过C作⊙O的切线,交AB的延长线于P,∠PCB=
如图,在△ABC中,以AC为直径的⊙O交BC于D,过C作⊙O的切线,交AB的延长线于P,∠PCB=| 1 |
| 2 |
(1)求证:AB=AC;
(2)若sin∠BAC=
| 3 |
| 5 |
考点:切线的性质
专题:
分析:(1)连接AD,由切线的性质及圆周角定理可证明∠CAD=∠BAD,可证明∠ABC=∠ACB,可证明AB=AC;
(2)过B作BE⊥AC于点E,可得∠PCB=∠CBE,在Rt△ABE和△BCE中可求得tan∠PCB.
(2)过B作BE⊥AC于点E,可得∠PCB=∠CBE,在Rt△ABE和△BCE中可求得tan∠PCB.
解答:(1)证明:如图1,连接AD,
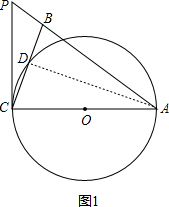
∵AC为直径,PC为⊙O的切线,
∴∠PCA=∠CDA=90°,
∴∠PCB+∠DCA=∠DCA+∠DAC,
∴∠PCB=∠DAC,
又∵∠PCB=
∠BAC,
∴∠BAD=∠PCB,
∴∠DAC=∠DAB,
∴∠ABC=∠ACB,
∴AB=AC;
(2)解:如图2,过B作BE⊥AC于点E,
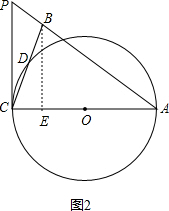
∵sin∠BAC=
,
∴可设BE=3x,则AB=5x,
在Rt△ABE中,由勾股定理可求得AE=4x,
又∵AC=AB=5x,
∴CE=AC-AE=5x-4x=x,
∴tan∠CBE=
=
,
又∵PC⊥AC,
∴BE∥PC,
∴∠CBE=∠PCB,
∴tan∠PCB=
.

∵AC为直径,PC为⊙O的切线,
∴∠PCA=∠CDA=90°,
∴∠PCB+∠DCA=∠DCA+∠DAC,
∴∠PCB=∠DAC,
又∵∠PCB=
| 1 |
| 2 |
∴∠BAD=∠PCB,
∴∠DAC=∠DAB,
∴∠ABC=∠ACB,
∴AB=AC;
(2)解:如图2,过B作BE⊥AC于点E,

∵sin∠BAC=
| 3 |
| 5 |
∴可设BE=3x,则AB=5x,
在Rt△ABE中,由勾股定理可求得AE=4x,
又∵AC=AB=5x,
∴CE=AC-AE=5x-4x=x,
∴tan∠CBE=
| CE |
| BE |
| 1 |
| 3 |
又∵PC⊥AC,
∴BE∥PC,
∴∠CBE=∠PCB,
∴tan∠PCB=
| 1 |
| 3 |
点评:本题主要考查切线的性质及等腰三角形的判定和三角函数的定义,掌握过切点的半径与切线垂直是解题的关键,在(2)中注意三角函数的定义.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
(a2)3等于( )
| A、3a2 |
| B、a5 |
| C、a6 |
| D、a8 |
已知下列命题:①若|a|=|b|,则
=
,②对角线相等的梯形是等腰梯形,③平分弦的直径垂直于弦,④对角线垂直且相等的四边形是正方形,其中原命题和逆命题均为真命题的个数是( )
| a |
| b |
| A、1 | B、2 | C、3 | D、4 |
式子
的取值范围是( )
| ||
| x+2 |
| A、x≥1 |
| B、x>1且x≠-2 |
| C、x≠-2 |
| D、x≥1 且 X≠-2 |
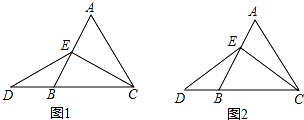
 如图所示,由条件∠A+∠B=180°,可判定哪两条直线平行?
如图所示,由条件∠A+∠B=180°,可判定哪两条直线平行?