题目内容
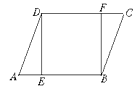
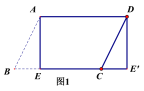
【题目】(1)如图1,纸片![]() ABCD中,AD=5,
ABCD中,AD=5,![]() ,过点A作AE⊥BC,垂足为E,沿AE剪下
,过点A作AE⊥BC,垂足为E,沿AE剪下![]() ,将它平移至
,将它平移至![]() 的位置,拼成四边形
的位置,拼成四边形![]() ,则四边形
,则四边形![]() 的形状为(_____)
的形状为(_____)
A.平行四边形 B.菱形 C.矩形 D.正方形
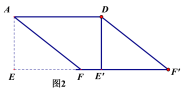
(2)如图2,在(1)中的四边形![]() 中,在EF上取一点P,EP=4,剪下
中,在EF上取一点P,EP=4,剪下![]() ,将它平移至
,将它平移至![]() 的位置,拼成四边形
的位置,拼成四边形![]() 。①求证:四边形
。①求证:四边形![]() 是菱形;②求四边形
是菱形;②求四边形![]() 的两条对角线的长。
的两条对角线的长。
【答案】C
【解析】
(1)根据矩形的判定方法即可判定;
(2)①通过计算证明AF=AD=5,证明四边形AFF′D是平行四边形即可;
②连接AF',DF,分别利用勾股定理计算即可;
(1)解:如图1中,
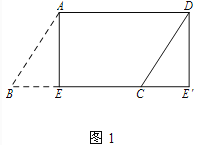
∵四边形ABCD是平行四边形,
∴AD=BC,
∵BE=CE′,
∴AD∥EE′,AD=EE′,
∴四边形AEE′D是平行四边形,
∵∠AEE′=90°,
∴四边形AEE′D是矩形,
故选C.
(2)如图2中,
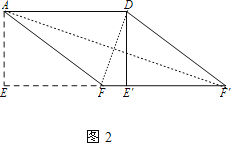
①证明:∵AD=5,S□ABCD=15,
∴AE=3.
又∵在图2中,EF=4,
∴在Rt△AEF中,AF═5.
∴AF=AD=5,
又∵AF∥DF',AF=DF,
∴四边形AFF′D是平行四边形.
∴四边形AFF′D是菱形.
②解:连接AF′,DF,
在Rt△DE′F中,
∵E′F=E′E-EF=5-4=1,DE′=3,
∴DF=![]()
在Rt△AEF′中,
∵E′F=E′E+E′F′=5+4=9,AE=3,
∴AF′=![]()

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目