Question

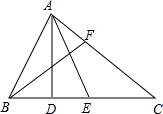
已知AD⊥BC，BE=CE，∠ABC=2∠C，BF为∠B的平分线．求证：AB=2DE．

 

 

Answer 1

【答案】

证明见解析.

【解析】

试题分析：连接EF．根据角平分线的性质知AF：FC=DE：EC，由平行线分线段成比例知AF：FC=DE：EC，由这两个比例式和已知条件“BE=CE”知，即AB=2DE．

试题解析: 连接EF．

∵∠ABC=2∠C，BF为∠B的平分线，

∴∠FBC=∠C=∠ABC，

∴BF=CF；

又∵BE=CE，

∴EF⊥BC；

∵AD⊥BC，

∴EF∥AD，

∴AF：FC=DE：EC；

而AB：BC=AF：FC，

∴AB：BC=DE：EC，

∴，

即AB=2DE．

考点: 1.平行线分线段成比例；2.角平分线的性质；3.等腰三角形的判定与性质.