题目内容
△ABC中,三个内角的度数比是1:1:2,最短的边长为3,则最长的边长为
- A.

- B.

- C.

- D.18
C
分析:由△ABC中,三个内角的度数比是1:1:2,可得出三角形的三个角的度数分别是45°、45°、90°,所以,两条直角边的长分别是3、3,根据勾股定理,可求得最长边即斜边的长.
解答:根据三角形的内角和定理,
∵△ABC中,三个内角的度数比是1:1:2,
∴180°× =45°,180°×
=45°,180°× =90°,
=90°,
即△ABC是等腰直角三角形,
∴两条直角边的长是3,
根据勾股定理得,最长边的长为:
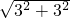 =
= ;
;
故选C.
点评:本题考查了等腰直角三角形,熟练应用三角形的内角和定理、勾股定理是解答本题的关键.
分析:由△ABC中,三个内角的度数比是1:1:2,可得出三角形的三个角的度数分别是45°、45°、90°,所以,两条直角边的长分别是3、3,根据勾股定理,可求得最长边即斜边的长.
解答:根据三角形的内角和定理,
∵△ABC中,三个内角的度数比是1:1:2,
∴180°×
 =45°,180°×
=45°,180°× =90°,
=90°,即△ABC是等腰直角三角形,
∴两条直角边的长是3,
根据勾股定理得,最长边的长为:
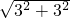 =
= ;
;故选C.
点评:本题考查了等腰直角三角形,熟练应用三角形的内角和定理、勾股定理是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
△ABC中,三个内角的度数比是1:1:2,最短的边长为3,则最长的边长为( )
A、
| ||
B、
| ||
C、
| ||
| D、18 |
 如图,在△ABC中,三个内角的角平分线交于点O,OE⊥BC于点E.
如图,在△ABC中,三个内角的角平分线交于点O,OE⊥BC于点E.