题目内容
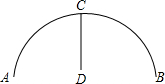 如图:圆弧形桥拱的跨度AB是12米,拱高CD(弧的中点到弦的距离)为4米,求拱桥所在圆的半径.
如图:圆弧形桥拱的跨度AB是12米,拱高CD(弧的中点到弦的距离)为4米,求拱桥所在圆的半径.
解:如图,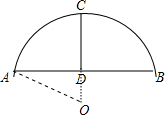 设圆的半径为R米,
设圆的半径为R米,
∵CD平分弧AB,且CD⊥AB,
∴圆心O在CD的延长线上,
∴CD平分AB,
∴AD= AB=6,
AB=6,
连OA,
在Rt△OAD中,AD=6,OA=R,OD=R-CD=R-4,
∵OA2=OD2+AD2,
∴R2=62+(R-4)2,
解得R= ,
,
即拱桥所在圆的半径 米.
米.
分析:设圆的半径为R米,由于CD平分弧AB,且CD⊥AB,根据垂径定理的推论得到圆心O在CD的延长线上,再根据垂径定理得到CD平分AB,则AD= AB=6,在Rt△OAD中,利用勾股定理可计算出半径R.
AB=6,在Rt△OAD中,利用勾股定理可计算出半径R.
点评:本题考查了垂径定理的应用:先把实际问题中的数据与几何图形中的量对应起来,然后根据垂径定理及其推论进行证明或计算.
 设圆的半径为R米,
设圆的半径为R米,∵CD平分弧AB,且CD⊥AB,
∴圆心O在CD的延长线上,
∴CD平分AB,
∴AD=
 AB=6,
AB=6,连OA,
在Rt△OAD中,AD=6,OA=R,OD=R-CD=R-4,
∵OA2=OD2+AD2,
∴R2=62+(R-4)2,
解得R=
 ,
,即拱桥所在圆的半径
 米.
米.分析:设圆的半径为R米,由于CD平分弧AB,且CD⊥AB,根据垂径定理的推论得到圆心O在CD的延长线上,再根据垂径定理得到CD平分AB,则AD=
 AB=6,在Rt△OAD中,利用勾股定理可计算出半径R.
AB=6,在Rt△OAD中,利用勾股定理可计算出半径R.点评:本题考查了垂径定理的应用:先把实际问题中的数据与几何图形中的量对应起来,然后根据垂径定理及其推论进行证明或计算.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目

 5、如图,圆弧形桥拱的跨度AB=12米,拱高CD=4米,则拱桥的半径为( )
5、如图,圆弧形桥拱的跨度AB=12米,拱高CD=4米,则拱桥的半径为( )
 23、如图,圆弧形桥拱的跨度AB=12米,拱高CD=4米,则拱桥的半径为多少?
23、如图,圆弧形桥拱的跨度AB=12米,拱高CD=4米,则拱桥的半径为多少? 如图:圆弧形桥拱的跨度AB是12米,拱高CD(弧的中点到弦的距离)为4米,求拱桥所在圆的半径.
如图:圆弧形桥拱的跨度AB是12米,拱高CD(弧的中点到弦的距离)为4米,求拱桥所在圆的半径.