题目内容
 如图所示,Rt△AOB中,O为坐标原点,∠AOB=90°,∠B=30°,若点A在反比例函数y=
如图所示,Rt△AOB中,O为坐标原点,∠AOB=90°,∠B=30°,若点A在反比例函数y=| 1 | x |
分析:分别过点A、B作y轴的垂线,垂足为M、N,由∠AOB=90°可知∠AOM+∠BON=90°,再根据∠AOM+∠MAO=90°可得出∠MAO=∠BON,故可得出△AOM∽△OBN,设A(a,
),B(x,y),再根据相似三角形的对应边成比例即可求出xy的值,进而得出结论.
| 1 |
| a |
解答: 解:分别过点A、B作y轴的垂线,垂足为M、N,
解:分别过点A、B作y轴的垂线,垂足为M、N,
∵∠AOB=90°,
∴∠AOM+∠BON=90°
又∵∠AOM+∠MAO=90°,
∴∠MAO=∠BON.
又∵∠AMO=∠BNO=90°,
∴△AOM∽△OBN,
设A(a,
),B(x,y)
∵△AOM∽△OBN,
∴
=
=
=
,
∴-y=
a,x=
∴xy=-3,
∴y=
(x>0).
 解:分别过点A、B作y轴的垂线,垂足为M、N,
解:分别过点A、B作y轴的垂线,垂足为M、N,∵∠AOB=90°,
∴∠AOM+∠BON=90°
又∵∠AOM+∠MAO=90°,
∴∠MAO=∠BON.
又∵∠AMO=∠BNO=90°,
∴△AOM∽△OBN,
设A(a,
| 1 |
| a |
∵△AOM∽△OBN,
∴
| a |
| -y |
| ||
| x |
| OA |
| OB |
| 1 | ||
|
∴-y=
| 3 |
| ||
| a |
∴xy=-3,
∴y=
| -3 |
| x |
点评:本题考查的是反比例函数综合题,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 如图所示,Rt△ABO的直角顶点在原点,OA=6,AB=10,AO与x轴正半轴的夹角为30°,求A、B两点坐标.
如图所示,Rt△ABO的直角顶点在原点,OA=6,AB=10,AO与x轴正半轴的夹角为30°,求A、B两点坐标. 一半?若存在,求出CP的长;若不存在,请说明理由.
一半?若存在,求出CP的长;若不存在,请说明理由.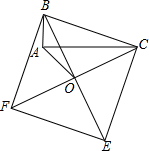 如图所示,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO,如果AB=4,AO=6
如图所示,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO,如果AB=4,AO=6 如图所示,Rt△ABO的直角顶点在原点,OA=6,AB=10,AO与x轴正半轴的夹角为30°,求A、B两点坐标.
如图所示,Rt△ABO的直角顶点在原点,OA=6,AB=10,AO与x轴正半轴的夹角为30°,求A、B两点坐标.