题目内容
【题目】如图，在Rt△ABC中，∠B=90°，∠A=30°，以点A为圆心，BC长为半径画弧交AB于点D，分别以点A、D为圆心，AB长为半径画弧，两弧交于点E，连接AE，DE，则∠EAD的余弦值是（ ）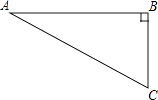
A.
B.
C.
D.
【答案】B
【解析】解：如图所示：
设BC=x，
∵在Rt△ABC中，∠B=90°，∠A=30°，
∴AC=2BC=2x，AB= 
BC= x，
根据题意得：AD=BC=x，AE=DE=AB= x，
作EM⊥AD于M，则AM= 
AD= x，
在Rt△AEM中，cos∠EAD= 
= 
= 
；
故答案为：B．
在Rt△ABC中，根据在直角三角形中，30度角所对的边是斜边的一半和勾股定理，求出AC=2BC，AB的代数式，在Rt△AEM中，求出cos∠EAD的值.
练习册系列答案
同步练习强化拓展系列答案
相关题目
