题目内容
直线 分别与x,y轴交点为C,A,BC=AC,AE平分∠CAO,OD平分∠AOC交AE于点D,连接BD交y轴于点F,点P从点B出发沿线段BC匀速运动,速度为5单位/秒,同时点Q从点C出发沿线段CA匀速运动,速度为5单位/秒,设点P,Q的运动时间为t秒.
分别与x,y轴交点为C,A,BC=AC,AE平分∠CAO,OD平分∠AOC交AE于点D,连接BD交y轴于点F,点P从点B出发沿线段BC匀速运动,速度为5单位/秒,同时点Q从点C出发沿线段CA匀速运动,速度为5单位/秒,设点P,Q的运动时间为t秒.(1)求线段BE的长.
(2)若△PEQ的面积为S,在点P,Q的运动过程中,求S与t的函数关系式,直接写出自变量t的取值范围.

【答案】分析:(1)分别把x=0和y=0代入一次函数解析式,求出OA、OC值,求出AC、BC,得出OB的值,根据角平分线性质求出OE,即可求出BE;
(2)过Q作QM⊥OC于M,分为两种情况:当P在BE上时,求出QM,根据三角形的面积公式求出即可;当P在CE上时,根据三角形的面积公式求出即可.
解答: 解:(1)∵
解:(1)∵ ,
,
∴当x=0时,y=6,
当y=0时,x=8,
∴A(0,6),C(8,0),
∴OA=6,OC=8,
在Rt△AOC中,由勾股定理得:AC= =10,
=10,
∵BC=AC,
∴OB=10-8=2,
∴B(-2,0),
∵AE平分∠CAO,
∴ =
= ,
,
∴ =
= ,
,
∴OE=3,
∴BE=2+3=5.
答:BE长是5;
(2)过Q作QM⊥OC于M,
根据题意得:CQ=5t,
∵sin∠ACB= =
= =
= ,
,
∴QM=3t,
当P在线段BE上时,即0<t<1,S△PQE= ×PE×QM=
×PE×QM= ×(5-5t)×3t=-
×(5-5t)×3t=- t2+
t2+ t;
t;
当P在EC上时,即1<t≤2,S= ×PE×QM=
×PE×QM= ×(5t-5)×3t=
×(5t-5)×3t= t2-
t2- t;
t;
综合上述:S与t的函数关系式是: .
.
点评:本题考查了一次函数图象上点的坐标特征,三角形的面积,解直角三角形,角平分线性质的应用,通过做此题培养了学生的分析问题和解决问题的能力,题目比较典型,是一道比较好的题目.
(2)过Q作QM⊥OC于M,分为两种情况:当P在BE上时,求出QM,根据三角形的面积公式求出即可;当P在CE上时,根据三角形的面积公式求出即可.
解答:
 解:(1)∵
解:(1)∵ ,
,∴当x=0时,y=6,
当y=0时,x=8,
∴A(0,6),C(8,0),
∴OA=6,OC=8,
在Rt△AOC中,由勾股定理得:AC=
 =10,
=10,∵BC=AC,
∴OB=10-8=2,
∴B(-2,0),
∵AE平分∠CAO,
∴
 =
= ,
,∴
 =
= ,
,∴OE=3,
∴BE=2+3=5.
答:BE长是5;
(2)过Q作QM⊥OC于M,

根据题意得:CQ=5t,
∵sin∠ACB=
 =
= =
= ,
,∴QM=3t,
当P在线段BE上时,即0<t<1,S△PQE=
 ×PE×QM=
×PE×QM= ×(5-5t)×3t=-
×(5-5t)×3t=- t2+
t2+ t;
t;当P在EC上时,即1<t≤2,S=
 ×PE×QM=
×PE×QM= ×(5t-5)×3t=
×(5t-5)×3t= t2-
t2- t;
t;综合上述:S与t的函数关系式是:
 .
.点评:本题考查了一次函数图象上点的坐标特征,三角形的面积,解直角三角形,角平分线性质的应用,通过做此题培养了学生的分析问题和解决问题的能力,题目比较典型,是一道比较好的题目.

练习册系列答案
相关题目
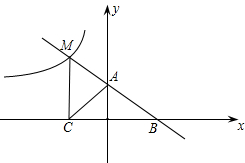 象限内的一点,且MC⊥x轴,C点为垂足,△AMC的面积为4.
象限内的一点,且MC⊥x轴,C点为垂足,△AMC的面积为4.
 y轴交于C、D两点.
y轴交于C、D两点. 如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A、C分别在坐标轴上,顶点B的坐标为(6,4),E为AB的中点,过点D(8,0)和点E的直线分别与BC、y轴交于点F、G.
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A、C分别在坐标轴上,顶点B的坐标为(6,4),E为AB的中点,过点D(8,0)和点E的直线分别与BC、y轴交于点F、G.