题目内容
已知:直线y=-x+2分别与y、x轴交于A、B两点,点M是该直线上在第二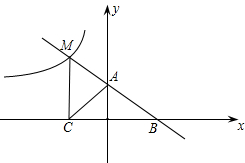 象限内的一点,且MC⊥x轴,C点为垂足,△AMC的面积为4.
象限内的一点,且MC⊥x轴,C点为垂足,△AMC的面积为4.(1)求点M的坐标;
(2)求过点M的反比例函数解析式.
分析:(1)用一个未知数设出点M的坐标,表示出△AMC的面积,即可求得点M的坐标;
(2)把点M坐标代入反比例函数解析式即可求得求过点M的反比例函数解析式.
(2)把点M坐标代入反比例函数解析式即可求得求过点M的反比例函数解析式.
解答:解:(1)∵点M在直线y=-x+2上,
∴设M(x,-x+2),
易得A(0,2),B(2,0),
∵△AMC的面积为4,
∴S△BCM-S△ABC=4,
∴
×(2-x)×(2-x)-
×(2-x)×2=4.
解得x=-2,
∴M(-2,4);
(2)设所求的函数解析式为y=
,
∴k=-2×4,
∴y=-
.
∴设M(x,-x+2),
易得A(0,2),B(2,0),
∵△AMC的面积为4,
∴S△BCM-S△ABC=4,
∴
| 1 |
| 2 |
| 1 |
| 2 |
解得x=-2,
∴M(-2,4);
(2)设所求的函数解析式为y=
| k |
| x |
∴k=-2×4,
∴y=-
| 8 |
| x |
点评:点在函数解析式上,那么点的横纵坐标适合这个函数解析式;反比例函数的比例系数等于它上面的点的横纵坐标的积.

练习册系列答案
相关题目
已知:直线y=-
x+
(n为正整数)与两坐标轴围成的三角形面积为Sn,则S1+S2+S3+…+S2011=( )
| n |
| n+1 |
| ||
| n+1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 19、如图,已知两直线a,b相交于O,∠2=30°,则∠1=
19、如图,已知两直线a,b相交于O,∠2=30°,则∠1= 已知:直线y=-2x+4交x轴于点A,交y轴于点B,点C为x轴上一点,AC=1,且OC<OA.抛物线y=ax2+bx+c(a≠0)经过点A、B、C.
已知:直线y=-2x+4交x轴于点A,交y轴于点B,点C为x轴上一点,AC=1,且OC<OA.抛物线y=ax2+bx+c(a≠0)经过点A、B、C.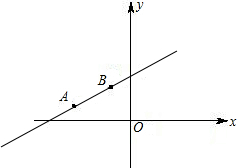 已知:直线y=kx+b的图象过点A(-3,1);B(-1,2),
已知:直线y=kx+b的图象过点A(-3,1);B(-1,2),