题目内容
已知,如图AB两侧是两个等腰三角形,其中等腰△ABC的底AB是等腰△ABD的腰。
(1)若∠CAD=120°,∠CBD=150°,求∠C,∠D;
(2)若∠CAD=90°,AC=AD,依题意画出符合条件的图形,并求∠C,∠D。
(1)若∠CAD=120°,∠CBD=150°,求∠C,∠D;
(2)若∠CAD=90°,AC=AD,依题意画出符合条件的图形,并求∠C,∠D。

解:(1)设∠C=x°,∠D=y°,
∵∠CAD=120°,∠CBD=150°,
∴∠C+∠D=360°﹣270°=90°,
∴x+y=90°①
∵△ABC是等腰三角形,
∴AC=BC,
∴∠CAB=∠CBA= ,
,
∵△ABD是等腰三角形,
∴AB=AD,
∴∠D=∠ABD=y°,
∴ +y=150°②
+y=150°②
有①②解得:x=20°,y=70°,
∴∠C=20°,∠D=70°;
(2)依题意画出符合条件的图形如图所示:

∵AC=AD=AB=BC,
∴△ACB是等边三角形,
∴∠C=60°,
∵∠CAD=90°,
∴∠BAD=30°,
∵AB=AD,
∴∠D= =75°,
=75°,
∴∠C=60°,∠D=75°。

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
 已知,如图AB两侧是两个等腰三角形,其中等腰△ABC的底AB是等腰△ABD的腰,
已知,如图AB两侧是两个等腰三角形,其中等腰△ABC的底AB是等腰△ABD的腰,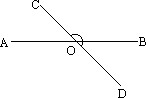

 已知,如图AB两侧是两个等腰三角形,其中等腰△ABC的底AB是等腰△ABD的腰,
已知,如图AB两侧是两个等腰三角形,其中等腰△ABC的底AB是等腰△ABD的腰,