题目内容
若p+q=0，抛物线y=x2+px+q必过点（ ）
分析：将x=1代入y=x2+px+q，得y=1+p+q，即y=1，由此确定选择项．
解答：解：∵y=x2+px+q，
∴当x=1时，y=1+p+q，
又∵p+q=0，
∴y=1，
即抛物线y=x2+px+q必过点（1，1）．
故选D．
∴当x=1时，y=1+p+q，
又∵p+q=0，
∴y=1，
即抛物线y=x2+px+q必过点（1，1）．
故选D．
点评：本题考查二次函数图象上点的坐标特征，图象经过点，点的坐标一定满足函数的解析式．
练习册系列答案
相关题目
如图，已知抛物线P：y=ax2+bx+c（a≠0）与x轴交于A、B两点（点A在x轴的正半轴上），与y轴交于点C，矩形DEFG的一条边DE在线段AB上，顶点F、G分别在线段BC、AC上，抛物线P上部分点的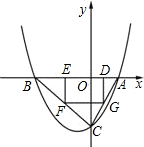
横坐标对应的纵坐标如下：
（1）求A、B、C三点的坐标；
（2）若点D的坐标为（m，0），矩形DEFG的面积为S，求S与m的函数关系，并指出m的取值范围；
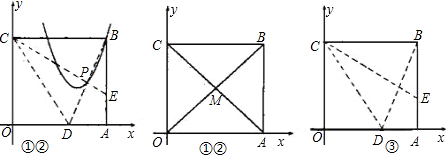
（3）当矩形DEFG的面积S取最大值时，连接DF并延长至点M，使FM=k•DF，若点M不在抛物线P上，求k的取值范围．
横坐标对应的纵坐标如下：| x | … | -3 | -2 | 1 | 2 | … | ||||
| y | … | -
|
-4 | -
|
0 | … |
（2）若点D的坐标为（m，0），矩形DEFG的面积为S，求S与m的函数关系，并指出m的取值范围；
（3）当矩形DEFG的面积S取最大值时，连接DF并延长至点M，使FM=k•DF，若点M不在抛物线P上，求k的取值范围．
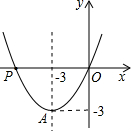
（2011•资阳）已知抛物线C：y=ax2+bx+c（a＜0）过原点，与x轴的另一个交点为B（4，0），A为抛物线C的顶点．