题目内容
10.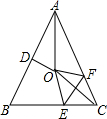 如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与线段AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠AOF的度数是( )
如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与线段AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠AOF的度数是( )| A. | 105° | B. | 110° | C. | 115° | D. | 120° |
分析 连接OB,根据中垂线的性质就可以得出AO=BO,就有∠OAB=∠OBA,根据角平分线的性质就可以求出∠EBO的度数,通过△ABO≌△ACO就有BO=CO,就有∠OBC=∠OCB,再由轴对称就可以求出OF=CF,求得∠FCO=∠FOC=25°,利用三角形的外角得出∠AFO=50°,进一步利用三角形的内角和求出结论.
解答 解:如图,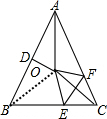
连接OB,
∵OD垂直平分AB,
∴AO=BO,
∴∠OAB=∠OBA.
∵AB=AC,∠BAC=50°
∴∠ABC=∠ACB=65°.
∵OA平分∠BAC,
∴∠BAO=∠CAO=$\frac{1}{2}$∠BAC=25°,
∴∠OBA=25°,
∴∠OBC=40°.
在△ABO和△ACO中
$\left\{\begin{array}{l}{AB=AC}\\{∠BAO=∠CAO}\\{AO=AO}\end{array}\right.$,
∴△ABO≌△ACO(SAS),
∴BO=CO,
∴∠OBC=∠OCB=40°.
∵△EOF与△ECF关于EF对称,
∴△EOF≌△ECF,
∴OF=CF,
∴∠FCO=∠FOC=25°.
∴∠AFO=50°,
∴∠AOF=180°-∠OAF-∠AFO=105°.
故选:A.
点评 本题考查了等腰三角形的性质的运用,中垂线的性质的运用,全等三角形的判定及性质的运用,轴对称的性质的运用,解答时运用全等三角形的性质及轴对称的性质求解是关键.

练习册系列答案
相关题目
20.下列三角形中,不是直角三角形的是( )
A.△ABC中,∠C-∠B=∠A;B.△ABC中,a:b:c=$1:\sqrt{2}:3$;C.△ABC中,(c-a)(c+a)=b2;D.△ABC中,∠A:∠B:∠C=1:3:4.
A.△ABC中,∠C-∠B=∠A;B.△ABC中,a:b:c=$1:\sqrt{2}:3$;C.△ABC中,(c-a)(c+a)=b2;D.△ABC中,∠A:∠B:∠C=1:3:4.
| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
2.某市为了鼓励居民节约用水,采用分段计费的方法按月计算每户家庭的水费,月用水量不超过20立方米时,按2元/立方米计费;月用水量超过20立方米时,其中的20立方米仍按2元/立方米收费,超过部分按2.6元/立方米计费.
(1)如果小红家每月用水15吨,水费是30元,如果每月用水23吨,水费是47.8元
(2)如果字母x表示小红家每月用水的吨数,那么小红家每月的水费如何用x代数式表示.
(3)如果小明家第二季度交纳水费的情况如下:
小明家这个季度共用水多少立方米?
(1)如果小红家每月用水15吨,水费是30元,如果每月用水23吨,水费是47.8元
(2)如果字母x表示小红家每月用水的吨数,那么小红家每月的水费如何用x代数式表示.
(3)如果小明家第二季度交纳水费的情况如下:
| 月份 | 四月份 | 五月份 | 六月份 |
| 交费金额 | 30元 | 34元 | 47.8元 |
19.若关于x的一元一次不等式组$\left\{\begin{array}{l}{2x-m≤0}\\{-x<3}\end{array}\right.$有解,则m的取值范围为( )
| A. | m<-6 | B. | m≤-6 | C. | m>-6 | D. | m≥-6 |
 如图,△ABC∽△ADE,则∠BAD=∠EAC=∠EBC.
如图,△ABC∽△ADE,则∠BAD=∠EAC=∠EBC.