题目内容
如图,是将菱形ABCD以点O为中心按顺时针方向分别旋转90°,180°,270°后形成的图形.若∠BAD=60°,AB=2,则图中阴影部分的面积为 .
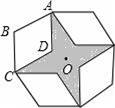

12﹣4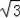
 .
.
【考点】旋转的性质;菱形的性质.
【分析】根据菱形的性质得出DO的长,进而求出S正方形DNMF,进而得出S△ADF即可得出答案.
【解答】解:如图所示:连接AC,BD交于点E,连接DF,FM,MN,DN,
∵将菱形ABCD以点O为中心按顺时针方向分别旋转90°,180°,270°后形成的图形,∠BAD=60°,AB=2,
∴AC⊥BD,四边形DNMF是正方形,∠AOC=90°,BD=2,AE=EC=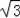
 ,
,
∴∠AOE=45°,ED=1,
∴AE=EO=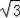
 ,DO=
,DO=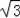
 ﹣1,
﹣1,
∴S正方形DNMF=2(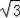
 ﹣1)×2(
﹣1)×2(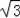
 ﹣1)×
﹣1)×
 =8﹣4
=8﹣4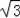
 ,
,
S△ADF=
 ×AD×AFsin30°=1,
×AD×AFsin30°=1,
∴则图中阴影部分的面积为:4S△ADF+S正方形DNMF=4+8﹣4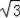
 =12﹣4
=12﹣4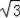
 .
.
故答案为:12﹣4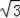
 .
.
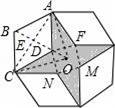

【点评】此题主要考查了菱形的性质以及旋转的性质,得出正确分割图形得出DO的长是解题关键.

练习册系列答案
相关题目




 ﹣a=
﹣a=
 ,且关于x的不等式组
,且关于x的不等式组
 只有4个整数解,那么b的取值范围是 .
只有4个整数解,那么b的取值范围是 .


 B.
B.
 C.
C.



