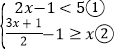题目内容
【题目】已知点![]() 都在直线
都在直线![]() 上,
上,![]() ,
,![]() 分别为
分别为![]() 中点,直线
中点,直线![]() 上所有线段的长度之和为19,则
上所有线段的长度之和为19,则![]() __________.
__________.
【答案】![]() 或4
或4
【解析】
根据点C与点B的位置关系分类讨论,分别画出对应的图形,推出各线段与AC的关系,根据直线![]() 上所有线段的长度之和为19,列出关于AC的方程即可求出AC.
上所有线段的长度之和为19,列出关于AC的方程即可求出AC.
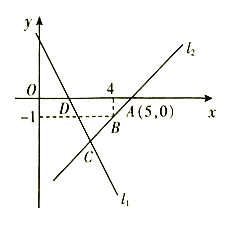
解:若点C在点B左侧时,如下图所示:
![]()
∵![]()
∴![]()
∴BC=![]() ,AB=
,AB=![]()
∵点![]() 分别为
分别为![]() 中点
中点
∴AD=DC=![]() ,CE=BE=
,CE=BE=![]()
∴AE=AC+CE=![]() ,DE=DC+CE=
,DE=DC+CE=![]() ,DB=DC+CB=AC
,DB=DC+CB=AC
∵直线![]() 上所有线段的长度之和为19
上所有线段的长度之和为19
∴AD+AC+AE+AB+DC+DE+DB+CE+CB+EB=19
即![]() +AC+
+AC+![]() +
+![]() +
+![]() +
+![]() +AC+
+AC+![]() +
+![]() +
+![]() =19
=19
解得:AC=![]() ;
;
若点C在点B右侧时,如下图所示:
∵![]()
∴![]()
∴BC=![]() ,AB=
,AB=![]()
∵点![]() 分别为
分别为![]() 中点
中点
∴AD=DC=![]() ,CE=BE=
,CE=BE=![]()
∴AE=AC-CE=![]() ,DE=DC-CE=
,DE=DC-CE=![]() ,DB=DC-CB=
,DB=DC-CB=![]()
∵直线![]() 上所有线段的长度之和为19
上所有线段的长度之和为19
∴AD+AC+AE+AB+DC+DE+DB+CE+CB+EB=19
即![]() +AC+
+AC+![]() +
+![]() +
+![]() +
+![]() +
+![]() +
+![]() +
+![]() +
+![]() =19
=19
解得:AC=![]()
综上所述:AC=![]() 或4.
或4.
故答案为:![]() 或4.
或4.

练习册系列答案
相关题目