题目内容
如图所示,在以O为圆心的两个同心圆中,小圆的半径为1,AB与小圆相切于点A,与大圆相交于点B,大圆的弦BC⊥AB于点B,过点C作大圆的切线CD交AB的延长线于点D,连接OC交小圆于点E,连接BE、BO.

(1)求证:△AOB∽△BDC;
(2)设大圆的半径为x,CD的长为y:
①求y与x之间的函数关系式;
②当BE与小圆相切时,求x的值.
答案:
解析:
解析:
|
(1)证明:如图,∵AB与小圆相切于点A,CD与大圆相交于点C, ∴∠OAB=∠OCD=90° ∵BC⊥AB ∴∠CBA=∠CBD=90° 1分 ∵∠1+∠OBC=90° ∠2+∠OCB=90° 又∵OC=OB ∴∠OBC=∠OCB ∴∠1=∠2 2分 ∴△AOB∽△BDC 3分
(2)解:①过点O作OF⊥BC于点F,则四边形OABF是矩形 4分 ∴BF=OA=1 由垂径定理,得BC=2BF=2 5分 在Rt△AOB中,OA=1,OB=x ∴AB= 由(1)得△AOB∽△BDC ∴ 即 ∴y= ②当BE与小圆相切时,OE⊥BE ∵OE=1,OC=x ∴EC=x-1 BE=AB= 在Rt△BCE中,EC2+BE2=BC2 即(x-1)2+( 解得:x1=2 x2=-1(舍去) 10分 ∴当BE与小圆相切时,x=2 11分 |

练习册系列答案
相关题目


 ) 7分
) 7分 53、如图所示,在以O为圆心的两个同心圆中,大圆的弦AB和CD相等,且AB与小圆相切于点E,求证:CD与小圆相切.
53、如图所示,在以O为圆心的两个同心圆中,大圆的弦AB和CD相等,且AB与小圆相切于点E,求证:CD与小圆相切.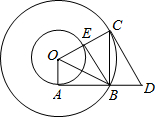 弦BC⊥AB于点B,过点C作大圆的切线CD交AB的延长线于点D,连接OC交小圆于点E,连接BE、BO.
弦BC⊥AB于点B,过点C作大圆的切线CD交AB的延长线于点D,连接OC交小圆于点E,连接BE、BO.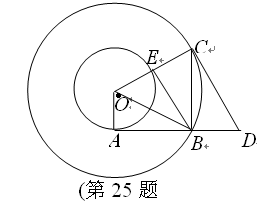
 A,与大圆相交于点B,大圆的弦BC⊥AB于点B,过点C作大圆的切线CD交AB的延长线于点D,连接OC交小圆于点E,连接BE、BO.
A,与大圆相交于点B,大圆的弦BC⊥AB于点B,过点C作大圆的切线CD交AB的延长线于点D,连接OC交小圆于点E,连接BE、BO.