题目内容
9.有一列数:a1,a2,a3,…,从第二个数开始,每一个数都等于1与它前面那个数的倒数的差,若a1=3,则a2016=-$\frac{1}{2}$.分析 根据题意,我们可以先求出这列数的前几个来寻找规律,当我们算出a4时,发现a4=a1,根据题中的运算法则,我们就能发现规律,从而得出结论.
解答 解:∵a1=3,a2=1-$\frac{1}{{a}_{1}}$=$\frac{2}{3}$,a3=1-$\frac{1}{{a}_{2}}$=-$\frac{1}{2}$,a4=1-$\frac{1}{{a}_{3}}$=3=a1,
∴a3n+1=a1,a3n+2,a3n+3=a3,(n∈N),
∵2016÷3=672,
∴a2016=a3=-$\frac{1}{2}$.
故答案为:-$\frac{1}{2}$.
点评 本题考查的规律的寻找,通过求出数列的几个数找出规律,解题的关键在于2016是3的整数倍.

练习册系列答案
相关题目
18.已知$\frac{2b}{3a-b}=\frac{3}{4}$,则$\frac{a}{b}$=( )
| A. | 6 | B. | $\frac{11}{9}$ | C. | $\frac{2}{15}$ | D. | $-\frac{2}{7}$ |
19.毕达哥拉斯学派对“数”与“形”的巧妙结合作了如下研究:
(1)六边形第5层的几何点数是17;第n层的几何点数是4n-3.
(2)在第6层时,六边形的几何点数是三角形的几何点数的3.5倍.
| 名称图形 几何 点数 | 三角形 | 正方形 | 五边形 | 六边形 |
 |  |  |  | |
| 第1层 | 1 | 1 | 1 | 1 |
| 第2层 | 2 | 3 | 4 | 5 |
| 第3层 | 3 | 5 | 7 | 9 |
| … | … | … | … | … |
| 第n层 |
(2)在第6层时,六边形的几何点数是三角形的几何点数的3.5倍.
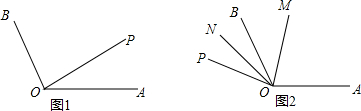
 如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.
如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°. 如图,AC,BD相交于点O,AC=BD,AB=CD,求证:OA=OD.
如图,AC,BD相交于点O,AC=BD,AB=CD,求证:OA=OD.