题目内容
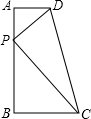 直角梯形ABCD中,∠A=∠B=90°,AB=7,AD=2,BC=3,在AB上取一点P,使△APD与△BPC相似,求AP的长.
直角梯形ABCD中,∠A=∠B=90°,AB=7,AD=2,BC=3,在AB上取一点P,使△APD与△BPC相似,求AP的长.
解:可设PA的长为x,
当△APD∽△BCP时,则 =
= ,即
,即 =
= ,解得x=1或x=6.
,解得x=1或x=6.
假设△APD∽△BPC,则 =
= ,即
,即 =
= ,
,
解得x= ;
;
综上所述,AP的长度为1、6或 .
.
分析:要使两个三角形相似,则可能是△APD∽△BPC,也可能是△APD∽△BCP,所以应分两种情况讨论,进而求解AP的值即可.
点评:本题主要考查了相似三角形的判定及性质问题,能够利用其性质求解一些简单的计算问题.
当△APD∽△BCP时,则
 =
= ,即
,即 =
= ,解得x=1或x=6.
,解得x=1或x=6.假设△APD∽△BPC,则
 =
= ,即
,即 =
= ,
,解得x=
 ;
;综上所述,AP的长度为1、6或
 .
.分析:要使两个三角形相似,则可能是△APD∽△BPC,也可能是△APD∽△BCP,所以应分两种情况讨论,进而求解AP的值即可.
点评:本题主要考查了相似三角形的判定及性质问题,能够利用其性质求解一些简单的计算问题.

练习册系列答案
相关题目
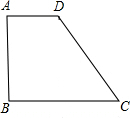 在直角梯形ABCD中,底AD=6cm,BC=11cm,腰CD=12cm,则这个直角梯形的周长为
在直角梯形ABCD中,底AD=6cm,BC=11cm,腰CD=12cm,则这个直角梯形的周长为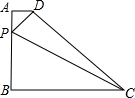 如图,直角梯形ABCD中,AD∥BC,∠B=90°,AD=1,BC=8,AB=6,点P在高AB上滑动,当AP长为
如图,直角梯形ABCD中,AD∥BC,∠B=90°,AD=1,BC=8,AB=6,点P在高AB上滑动,当AP长为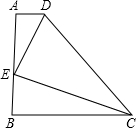 下结论:
下结论: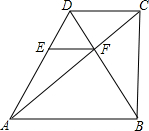 EF∥AB,交AD于点E,CF=4cm.
EF∥AB,交AD于点E,CF=4cm.