题目内容
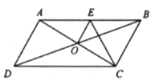
【题目】如图，平行四边形ABCD的对角线AC、BD相交于点O，∠ABC=60°，点E是AB的中点，连接CE、OE，若AB=2BC，下列结论：①∠ACD=30°；②当BC=4时,BD=
；③CD=4OE；④S△COE=
S四边形ABCD．其中正确的个数有（ ）
A.1B.2C.3D.4
【答案】C
【解析】
根据∠ABC=60°，点E是AB的中点，且AB=2BC判断出
是等边三角形，从而得出
，判断①；
过点B作
交DC于H，计算
长度，再根据勾股定理计算
判断②；
根据E，O分别为AB，BD的中点利用中位线定理和AB=2BC判断③；
通过中位线定理得出相似以及线段等量关系从而得出面积的关系判断④．
∵∠ABC=60°，点E是AB的中点，且AB=2BC
∴
∴是等边三角形，
∴
∴
,①正确；
过点B作交DC于H如图：
∵BC=4，
∴
∴
,②正确；
∵E，O分别为AB，BD的中点
∴
又∵
∴
,③正确；
∵OE为三角形ABC的中位线
∴
∴
设三角形EOM的面积为S，则三角形MOC面积为2S，三角形MBC面积为4S，三角形EMB面积为2S
∴三角形ABC面积为12S
∴平行四边形ABCD面积为24S
∴S△COE=
S四边形ABCD， ④错误
故答案选：C
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
【题目】（6分）小聪是个数学爱好者，他发现从1开始，连续几个奇数相加，和的变化规律如右表所示：
加数个数 | 连续奇数的和S |
1 | 1= |
2 | 1+3=22 |
3 | 1+3+5=32 |
4 | 1+3+5+7=42 |
5 | 1+3+5+7+9=52 |
n | … |
（1）如果n=7，则S的值为 ；
（2）求1+3+5+7+…+199的值；
（3）求13+15+17+…+79的值．
