Question

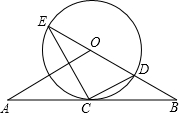（2012•遂溪县一模）如图，直线AB经过⊙O上的点C，并且OA=OB，CA=CB，⊙O交直线OB于E、D，连EC，CD
（1）试猜想直线AB于⊙O的位置关系，并说明理由；
（2）求证：BC²=BD•BE；
（3）若tan∠CED=

1

2

，⊙O的半径为3，求△OAB的面积．

Answer 1

分析：（1）连接OC，根据OA=OB，CA=CB，可以证明OC⊥AB，利用切线的判定定理，经过半径的外端，并且垂直于这条半径的直线是圆的切线，得到AB是⊙O的切线；
（2）根据ED是直径，直径所对的圆周角是直角，以及圆的切线垂直于过切点的半径，利用等量代换得到∠E=∠BCD，又∠B公共，可以证明△BCD∽△BEC，然后利用相似三角形的性质，对应线段的比相等得到BC²=BD•BE．
（3）根据△BCD∽△BEC，得BD与BC的比例关系，最后由切割线定理列出方程求出OA的长．在直角三角形AOC中，由勾股定理求得AC边的长度；最后由三角形的面积公式即可求得△OAB的面积．

解答：（1）解：直线AB是⊙O的切线．理由如下：
如图，连接OC．
∵OA=OB，CA=CB，
∴OC⊥AB．
又∵OC是⊙O的半径，
∴AB是⊙O的切线；

（2）证明一：∵ED是⊙O的直径，
∴∠ECD=90°（直径所对的圆周角是直角），
∴∠E+∠EDC=90°（直角三角形的两个锐角互余）．
又∵∠BCD+∠OCD=90°，∠OCD=∠ODC，
∴∠BCD=∠E．
又∵∠CBD=∠EBC，
∴△BCD∽△BEC．
∴

BC

BE

=

BD

BC

，
∴BC²=BD•BE；
证明二：由（1）知，BC是⊙O的切线．
∵BDE是⊙O的割线，
∴BC²=BD•BE；

（3）∵tan∠CED=

1

2

，
∴

CD

EC

=

1

2

．
由（2）知，△BCD∽△BEC，则

BC

BE

=

BD

BC

=

1

2

，
∴BC=2BD．
设BD=x，BC=2x．又BC²=BD•BE，∴（2x）²=x•（x+6），
解得x₁=0，x₂=2，
∵BD=x＞0，
∴BD=2，
∴OA=OB=BD+OD=3+2=5．
在Rt△OAC中，OA=5，OC=3，则根据勾股定理求得AC=4．
∴AB=2AC=8，
∴S_△OAB=

1

2

AB•OC=

1

2

×8×3=12，即△OAB的面积是12．

点评：本题考查了圆的综合题．其中涉及到的知识点有：
①切线的判定，例如：第（1）题，是利用等腰三角形底边上的中线也是底边上的高，得到OC⊥AB，证明AB是⊙O的切线；
②相似三角形的判定与性质．例如：第（2）题，是根据题意证明两个三角形相似，利用相似三角形的性质，得到线段BC，BD和BE的数量关系；
③三角形的面积公式；
④等腰三角形的性质．