题目内容
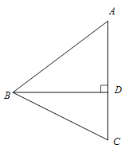
【题目】在纸面上有一数轴如图所示．
尝试：折叠纸面，使表示1的点与表示
的点重合，则表示
的点与表示_________的点重合．
发现：折叠纸面，使表示的点与表示3的点重合，则表示5的点与表示____________的点重合．
应用：若数轴上
、
两点之间的距离为11（在左侧），且经过折叠后，表示的点与表示3的点重合，点与点重合，分别求、两点表示的数．
【答案】尝试：3；发现：
；应用：点A表示的数为
，点B表示的数为
．
【解析】
尝试：先找出折痕点，再根据数轴的定义即可得；
发现：参照“尝试”的方法，先找出折痕点，再根据数轴的定义即可得；
应用：先根据数轴的定义得出A、B两点所表示的数的等式，再根据“表示
的点与表示3的点重合”找出折痕点，然后根据“折叠后点
与点
重合”求解即可得．
尝试：由表示1的点与表示的点重合得：折痕点表示的数为
则表示的点与表示3的点重合
故答案为：3；
发现：由表示的点与表示3的点重合得：折痕点表示的数为
设所求的数为x
则
解得
故答案为：；
应用：设、两点表示的数分别为
由题意得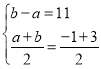
解得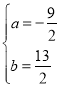
故点A表示的数为，点B表示的数为．
练习册系列答案
阅读快车系列答案
相关题目
