��Ŀ����
��һ����ʽ�ӡ�1+2+3+4+5+��+100����ʾ1��ʼ��100��������Ȼ���ĺͣ���������ʽ�ӱȽϳ�����дҲ�����㣬Ϊ�˼����������ǿ��Խ���1+2+3+4+5+��+100����ʾΪ �����
����� ������ͷ��ţ����磺1+3+5+7+9+��+99������1��ʼ��100���ڵ����������ĺͣ��ɱ�ʾΪ
������ͷ��ţ����磺1+3+5+7+9+��+99������1��ʼ��100���ڵ����������ĺͣ��ɱ�ʾΪ ��2n-1��������13+23+33+43+53+63+73+83+93+103�ɱ�ʾΪ
��2n-1��������13+23+33+43+53+63+73+83+93+103�ɱ�ʾΪ n3��ͨ�������Բ��ϵ��Ķ��������
n3��ͨ�������Բ��ϵ��Ķ�������� ��n2-1��=________������д���ļ�������
��n2-1��=________������д���ļ�������
50
��������
��������� ��n2��1��
��n2��1��
=��12��1��+��22��1��+��32��1��+��42��1��+��52��1��
=0+3+8+15+24
=50��
�ʴ�Ϊ��50��
���㣺�������Ļ������

��ϰ��ϵ�д�
�����Ŀ




 C��
C��

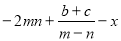 ��ֵ��
��ֵ��




 D��x1=0�� x2=3
D��x1=0�� x2=3