题目内容
已知⊙O的直径AB=2，弦AD=
，点C为⊙O上一点，∠CAD=15°，则sin∠CAB=________．
分析：存在两种情况，如图，C1、C2，根据题意，可得到AD=BD，即∠DAB=45°，求出∠CAB的度数即可解答．
解答：
解：如图，∵直径AB=2，弦AD=
，∴AD=BD=
，∴∠DAB=45°，又∠CAD=15°，
∴∠C1AB=60°，
∠C2AB=30°，
∴sin∠CAB=
；故答案为：
．点评：本题主要考查了特殊角的三角函数值，注意本题分两种情况解答．
练习册系列答案
名校课堂系列答案
相关题目
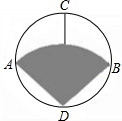某种商品的商标图案如图（图中的阴影部分），已知⊙O的直径AB⊥CD，且AB=8cm，弧AB是以D为圆心，DA为半径的弧，则商标图案的面积为
已知⊙O的直径AB=10，有一动点C从A点沿圆周顺时针向点B运动，若点D为弦AC所对弧的三等分点，过点D作DE⊥AB于E，直线AC交直线DB于G，点C、D都不与直径AB两端点重合，
如图，已知⊙O的直径AB与弦CD互相垂直，垂足为点E．⊙O的切线BF与弦AC的延长线相交于点F，且AC=8，tan∠BDC=