题目内容
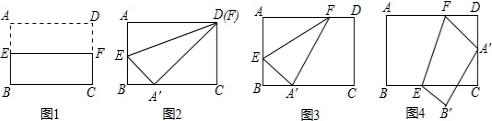
将矩形ABCD折叠,使得对角线的两个端点A、C重合,折痕所在直线交直线AB于点E,如果AB=4,BE=1,那么∠CAB的余切值是________.
 或
或
分析:本题是一道比较常见的折叠问题,需要注意题目中的“直线AB”与“折痕所在的直线”,显然,满足题意的情况有两种:①点E在线段AB上,如图1;②点E在线段AB的延长线上,如图2.因此需要分类讨论.
解答:
 解:①如图1,当点E在线段AB上时,过点P作PH⊥AB于点H.易得AH=BE=1,则HE=AB-2BE=2.
解:①如图1,当点E在线段AB上时,过点P作PH⊥AB于点H.易得AH=BE=1,则HE=AB-2BE=2.设BC=PH=x,易证△ABC∽△PHE,则
 =
= ,解得x=2
,解得x=2 ,此时,cot∠CAB=
,此时,cot∠CAB= ;
;②如图2,当点E在线段AB的延长线上时.过点P作PH⊥BC于点H.
易得PH=AB=4,
易得
 =
= =
= ,BQ=CH=
,BQ=CH= QH.
QH.设BC=t,则QH=
 t.
t.易证△ABC∽△QHP,则
 =
= ,解得t=2
,解得t=2 ,此时cot∠CAB=
,此时cot∠CAB= .
.综上所述,∠CAB的余切值是
 或
或 .
.故答案是:
 或
或 .
.点评:本题综合考查了相似三角形的判定与性质,折叠问题以及矩形的性质.解题时,一定要分类讨论,以防漏解.

练习册系列答案
相关题目
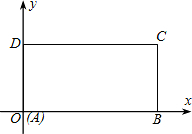 如图,在平面直角坐标系xoy中,已知矩形ABCD的边AB、AD分别在x轴、y轴上,点A与坐标原点重合,且AB=2,AD=1.
如图,在平面直角坐标系xoy中,已知矩形ABCD的边AB、AD分别在x轴、y轴上,点A与坐标原点重合,且AB=2,AD=1. 14、如图,在矩形ABCD中,AB=6cm,将矩形ABCD折叠,使点B与点D重合,点C落在C′处,若AE:BE=1:2,则折痕EF的长为
14、如图,在矩形ABCD中,AB=6cm,将矩形ABCD折叠,使点B与点D重合,点C落在C′处,若AE:BE=1:2,则折痕EF的长为 (2012•河池)如图,在矩形ABCD中,AD>AB,将矩形ABCD折叠,使点C与点A重合,折痕为MN,连接CN.若△CDN的面积与△CMN的面积比为1:4,则
(2012•河池)如图,在矩形ABCD中,AD>AB,将矩形ABCD折叠,使点C与点A重合,折痕为MN,连接CN.若△CDN的面积与△CMN的面积比为1:4,则