题目内容
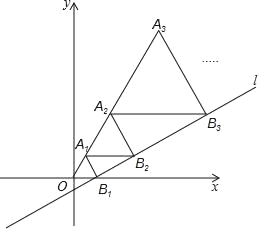
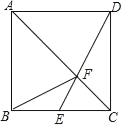
【题目】如图,已知正方形ABCD,点E是BC边的中点,DE与AC相交于点F,连接BF,下列结论:①△ABF≌△ADF;②S△ADF=2S△CEF;③tan∠EBF=![]() ;④S△ABF=4S△BEF,其中正确结论的个数是( )
;④S△ABF=4S△BEF,其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】分析:根据SAS可以推出△AFD≌△AFB,故①正确;即可推出S△ABF=S△ADF,由BE=EC=![]() BC=
BC=![]() AD,AD∥EC,推出
AD,AD∥EC,推出![]() =
=![]() ,可得S△ABF=S△ADF=4S△CEF,S△CEF=S△BEF,故②错误,④正确,求出CM=
,可得S△ABF=S△ADF=4S△CEF,S△CEF=S△BEF,故②错误,④正确,求出CM=![]() BC,即可判断③.
BC,即可判断③.
详解:∵四边形ABCD是正方形,
∴AD∥CB,AD=BC=AB,∠FAD=∠FAB,
在△AFD和△AFB中,
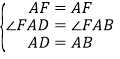 ,
,
∴△AFD≌△AFB,故①正确,
∴S△ABF=S△ADF,
∵BE=EC=![]() BC=
BC=![]() AD,AD∥EC,
AD,AD∥EC,
∴![]() =
=![]() ,
,
∴S△ADF=4S△CEF,S△CFE=4S△BEF,
故②错误;④正确;
延长BF交CD于M,
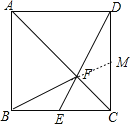
∵四边形ABCD是正方形,
∴AB∥CD,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴CM=![]() AB=
AB=![]() CD=
CD=![]() BC,
BC,
∴tan∠EBF=![]() =
=![]() ,故③正确;
,故③正确;
即正确的个数是3,
故选:C.

【题目】为了鼓励市民节约用水,某市居民生活用水按阶梯式水价计费.下表是该市民一户一表"生活用水阶梯式计费价格表的部分信息:
自来水销售价格 | 污水处理价格 | |
每户每月用水量 | 单价:元/吨 | 单价:元/吨 |
|
|
|
超过 |
|
|
超过 |
|
|
(说明:每户生产的污水量等于该户自来水用量;②水费=自来水费用+污水处理费)
已知小王家2018年7月用水![]() 吨,交水费
吨,交水费![]() 元.8月份用水
元.8月份用水![]() 吨,交水费
吨,交水费![]() 元.
元.
(1)求![]() 的值;
的值;
(2)如果小王家9月份上交水费![]() 元,则小王家这个月用水多少吨?
元,则小王家这个月用水多少吨?
(3)小王家10月份忘记了去交水费,当他11月去交水费时发现两个月一共用水50吨,其中10月份用水超过![]() 吨,一共交水费
吨,一共交水费![]() 元,其中包含
元,其中包含![]() 元滞纳金,求小王家11月份用水多少吨? (滞纳金:因未能按期缴纳水费,逾期要缴纳的“罚款金额”)
元滞纳金,求小王家11月份用水多少吨? (滞纳金:因未能按期缴纳水费,逾期要缴纳的“罚款金额”)
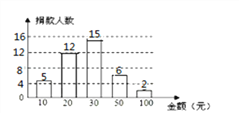
【题目】某市在今年对全市6000名八年级学生进行了一次视力抽样调查,并根据统计数据,制作了如图所示的统计表和统计图.
组别 | 视力 | 频数(人) |
|
| 20 |
|
|
|
|
|
|
|
| 70 |
|
| 10 |
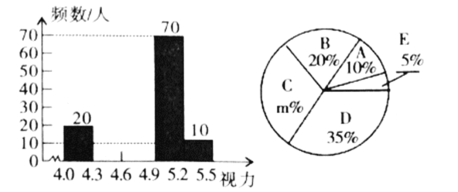
请根据图表信息回答下列问题:
(1)求抽样调查的人数;
(2)![]() ___________,
___________,![]() _____________,
_____________,![]() _____________;
_____________;
(3)补全频数分布直方图;
(4)若视力在4.9以上(含4.9)均属正常,则视力正常的人数占被统计人数的百分比是多少?