Question

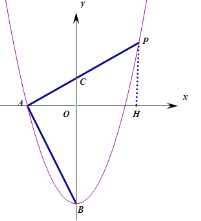
【题目】在平面直角坐标系中，抛物线与轴的负半轴交于点、与轴交于点，且.

（1）求的值；

（2）如果点是抛物线上一点，联结交轴正半轴于点，，求的坐标.

Answer 1

【答案】（1）1 （2）（4，12）

【解析】

（1）先根据y轴上点的坐标特征确定B（0，-4），再利用勾股定理计算出OA=2，则A点坐标为（-2，0），然后把A点坐标代入y=ax2-4求出a的值即可得到抛物线解析式；

（2）作PH⊥x轴于点H，则AH=x+3，PH∥BC,根据平行线分线段成比例定理求出点P的横坐标，进而可求出点P的坐标.

（1）当x=0时，y=ax2-4=-4，则B（0，-4），所以OB=4，

在Rt△OAB中，OA= =2，

∴A点坐标为（-2，0），

把A（-2，0）代入y=ax2-4得4a-4=0，

解得a=1;

（2∵a=1，

∴抛物线解析式为y=x2-4.

设P（x，x2-4）.

∵，

∴，

作PH⊥x轴于点H，则AH=x+3，PH∥BC,

∴,

∴，

∴x=4,

∴y= x2-4=12,

∴P（4，12）.