题目内容
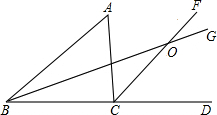如图所示，△ABC的外角∠ACD的平分线CF与∠ABC的平分线BG相交于点O．求证：点O到三边AB，BC，AC的距离相等．
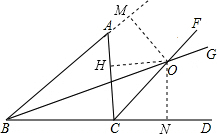证明：如图，过点O作OM⊥AB交BA的延长线于M，过点O作ON⊥BC于N，过点O作OH⊥AC于H，∵∠ACD的平分线CF与∠ABC的平分线BG相交于点O，
∴ON=0H，OM=ON，
∴OM=ON=OH，
即点O到三边AB，BC，AC的距离相等．
分析：过点O作OM⊥AB交BA的延长线于M，过点O作ON⊥BC于N，过点O作OH⊥AC于H，然后根据角平分线上的点到角的两边的距离相等可得OM=ON=OH，从而得证．
点评：本题考查了角平分线上的点到角的两边的距离相等的性质，熟记性质是解题的关键，作出图形更形象直观．
练习册系列答案
阅读快车系列答案
相关题目
（2012•内江）如图所示，△ABC的顶点是正方形网格的格点，则sinA的值为（ ）
如图所示，△ABC的三个顶点的坐标分别为A（4，3）、B（-2，1）、C（0，-1），则△ABC外接圆的圆心坐标是
如图所示为△ABC的各边，角的数据．利用全等三角形的条件，从中选取适当的数据，画出与△ABC全等的三角形，则方法共有（ ）
如图所示三角形ABC的面积为（ ）cm2．
如图所示，△ABC的顶点坐标分别是A（0，0）、B（6，0）、C（5，5）．