题目内容
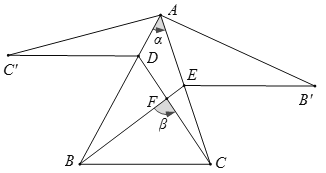
【题目】如图,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,与直线
,与直线![]() 相交于点
相交于点![]() .
.

(1)求点![]() 的坐标;
的坐标;
(2)请判断![]() 的形状并说明理由;
的形状并说明理由;
(3)动点![]() 从原点
从原点![]() 出发,以每秒
出发,以每秒![]() 个单位的速度沿着
个单位的速度沿着![]() 的路线向点
的路线向点![]() 匀速运动(
匀速运动(![]() 不与点
不与点![]() 、
、![]() 重合),过点
重合),过点![]() 分别作
分别作![]() 轴于
轴于![]() ,
,![]() 轴于
轴于![]() ,设运动
,设运动![]() 秒时,矩形
秒时,矩形![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
【答案】(1)![]() ;(2)等边三角形,见解析;(3)当
;(2)等边三角形,见解析;(3)当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
【解析】
(1)解两个函数解析式组成的方程组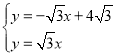 即可得到交点P的坐标;
即可得到交点P的坐标;
(2)过点P作PC⊥x轴于C,得到OC=2,PC=![]() ,AC=OA-OC=2,根据勾股定理求出OP=4,AP=4,得到AP=OP=OA,即可得到
,AC=OA-OC=2,根据勾股定理求出OP=4,AP=4,得到AP=OP=OA,即可得到![]() 是等边三角形的结论;
是等边三角形的结论;
(3)当![]() 时,OE=t,过点P作PC⊥x轴于C,根据EF∥PC,得到
时,OE=t,过点P作PC⊥x轴于C,根据EF∥PC,得到![]() ,求出EF=
,求出EF=![]() ,OF=
,OF=![]() ,得到
,得到![]() ;当
;当![]() 时,AE=8-t,BE交OP于M,根据EF∥PC,得到
时,AE=8-t,BE交OP于M,根据EF∥PC,得到![]() ,求出
,求出![]() ,
,![]() ,根据∠BMO=∠POA=60°,BO=
,根据∠BMO=∠POA=60°,BO=![]() 求出BM=
求出BM=![]() BO=
BO=![]() ,根据S=
,根据S=![]() 求出函数解析式.
求出函数解析式.
解:(1)解方程组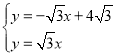 ,
,
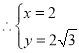 ,
,
![]() 点
点![]() 的坐标是
的坐标是![]() ;
;
(2)![]() 是等边三角形,
是等边三角形,
当![]() 时,
时,![]() ,
,
![]() 的坐标是
的坐标是![]() ,
,
过点P作PC⊥x轴于C,
∵P![]() ,
,
∴OC=2,PC=![]() ,
,
∴AC=OA-OC=2,
∵∠PCO=90°,
∴OP=![]() 4,
4,
同理AP=4,
∴AP=OP=OA,
∴![]() 是等边三角形;
是等边三角形;
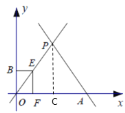
(3)当![]() 时,OE=t,
时,OE=t,
过点P作PC⊥x轴于C,
∵EF⊥x轴,
∴EF∥PC,
∴![]() ,
,
∴![]() ,
,
∴EF=![]() ,OF=
,OF=![]() ,
,
∴![]() ;
;
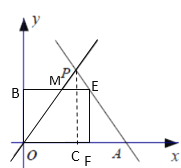
当![]() 时,AE=8-t,BE交OP于M,
时,AE=8-t,BE交OP于M,
∵EF∥PC,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵∠BMO=∠POA=60°,BO=![]() ,
,
∴BM=![]() BO=
BO=![]() ,
,
∴S=![]()
=![]()
=![]()
![]() .
.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目