题目内容
20.判定一个三角形是不是等腰三角形,我们经常利用以下的判定方法:“如果一个三角形有两个角相等,那么这两个角所对的边也相等”,请你利用以上判定方法解决下列问题如图1,在△ABC中,∠ACB=90°,∠B=30°,将△ABC绕顶点C顺时针旋转,旋转角为β(0°<β<180°),得到△A′B′C
(1)当旋转角为β=20°,∠A′B′C=30°;
(2)当AB∥CB′时,设A′B′与CB相交于点D,求证:D是A′B′的中点;
(3)如图2,E是AC边上的点,且AE=$\frac{1}{3}$AC,P是A′B′边上的点,且∠A′PC=60°,连接EP,已知AC=α,当β=120°时,EP长度最大,最大值为$\frac{5}{3}$a.
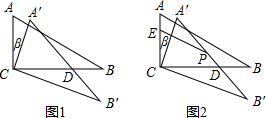
分析 (1)根据旋转的性质,旋转前后两个图形全等,则∠A'B'C=∠B,据此求解;
(2)根据平行的性质证明∠BCB'=∠B',然后证明∠A'DC=∠A',根据等角对等边即可证得;
(3)∠A′PC=60°时易证△A'CP是等边三角形,当A、C、P在一条直线上时,EP的长度最大,据此即可求解.
解答 解:(1)∠A'B'C=∠B=30°;
(2)∵AB∥CB′,
∴∠BCB'=∠B=30°,
又∵∠B'=30°,
∴∠BCB'=∠B'=30°,∠A'DC=∠BCB'+∠B'=60°,
∴CD=B'D,
∵∠CA'D=∠A'DC=60°,
∴A'D=CD,
∴A'D=B'D,即D是A'B'的中点;
(3)∵∠A′PC=60°,∠A'=∠A=60°,
∴△A'CP是等边三角形.
∴CP=CA'=a,∠A'CP=60°,
∴当β=180°-60°=120°时,EP长度最大,最大值为$\frac{2}{3}$a+a=$\frac{5}{3}$a.
故答案是:120,$\frac{5}{3}$a.
点评 本题考查了图形的旋转,旋转前后的两个图形全等,理解当A、C、P在一条直线上时,EP的长度最大是解决本题的关键.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
2.下列各式计算正确的是( )
| A. | 2(a+1)=2a+1 | B. | a3+a3=a6 | C. | -3a+2a=-a | D. | a2+a3=a5 |
3.对抛物线y=-x2+2x-3而言,下列结论正确的是( )
| A. | 与x轴有两个交点 | B. | 顶点坐标是(1,-2) | ||
| C. | 与y轴的交点坐标是(0,3) | D. | 开口向上 |
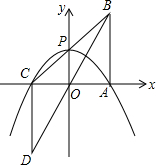 如图,已知△OAB的顶点坐标分别是0(0,0),A(1,0),B(1,2).将△OAB绕点O按逆时针方向旋转180°得到△OCD.
如图,已知△OAB的顶点坐标分别是0(0,0),A(1,0),B(1,2).将△OAB绕点O按逆时针方向旋转180°得到△OCD.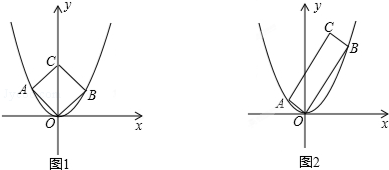
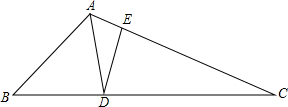 如图,已知△ABC,AD平分∠BAC,DE垂直AC,垂足为E,∠ADB=2∠B=4∠C,AE=$\frac{3}{4}$,CD=$\frac{7}{2}$,则线段AB=$\frac{55}{26}$.
如图,已知△ABC,AD平分∠BAC,DE垂直AC,垂足为E,∠ADB=2∠B=4∠C,AE=$\frac{3}{4}$,CD=$\frac{7}{2}$,则线段AB=$\frac{55}{26}$.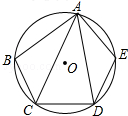 如图,在圆的内接五边形ABCDE中,∠B+∠E=220°,则∠CAD=40°.
如图,在圆的内接五边形ABCDE中,∠B+∠E=220°,则∠CAD=40°.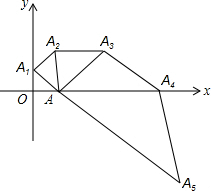 如图,已知△OAA1是腰长为1的等腰直角三角形,以Rt△OAA1的斜边AA1为直角边,画第二个等腰Rt△AA1A2,再以Rt△AA1A2为直角边,画第三个等腰Rt△AA2A3,…,以此类推,则点A2016的坐标是[-21008+1,($\sqrt{2}$)2015 ]..
如图,已知△OAA1是腰长为1的等腰直角三角形,以Rt△OAA1的斜边AA1为直角边,画第二个等腰Rt△AA1A2,再以Rt△AA1A2为直角边,画第三个等腰Rt△AA2A3,…,以此类推,则点A2016的坐标是[-21008+1,($\sqrt{2}$)2015 ]..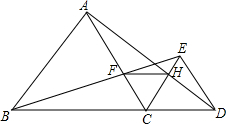 如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,
如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,