题目内容
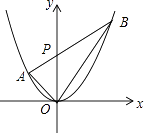
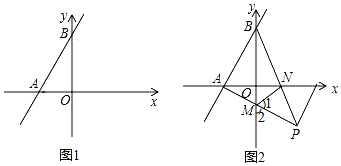
【题目】如图1,在平面直角坐标系中,直线AB分别交x轴、y轴于点![]() 点
点![]() 且a、b满足
且a、b满足![]() .
.
![]() ______;
______;![]() ______.
______.
![]() 点P在直线AB的右侧,且
点P在直线AB的右侧,且![]() ,
,
![]() 若点P在x轴上,则点P的坐标为______;
若点P在x轴上,则点P的坐标为______;
![]() 若
若![]() 为直角三角形,求点P的坐标;
为直角三角形,求点P的坐标;
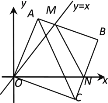
![]() 如图2,在
如图2,在![]() 的条件下,
的条件下,![]() 且点P在第四象限,AP与y轴交于点M,BP与x轴交于点N,连接
且点P在第四象限,AP与y轴交于点M,BP与x轴交于点N,连接![]() 求证:
求证:![]() 提示:过点P作
提示:过点P作![]() 交x轴于
交x轴于![]()
【答案】(1)![]() ,4;(2)
,4;(2)![]() ;
;![]() 或
或![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)![]() ,根据非负数的性质即可求解;
,根据非负数的性质即可求解;
(2)①点P在x轴上,则OP=OB=4,即可求解;②分∠BAP=90°、∠ABP=90°两种情况,求解即可;
![]() 通过证明△MEP≌△HFP(AAS)得:∠2=∠FHP,证明△MNP≌△HNP(SAS),∠1=∠NHP,即可求解.
通过证明△MEP≌△HFP(AAS)得:∠2=∠FHP,证明△MNP≌△HNP(SAS),∠1=∠NHP,即可求解.
解:![]() ,
,
即:![]() ,
,![]() ,
,
故答案是![]() ,4;
,4;
![]() 点P在x轴上,则
点P在x轴上,则![]() ,
,
故:答案是![]() ;
;
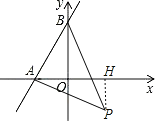
![]() 当
当![]() 时,
时,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,又
,又![]() ,
,
![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
故点P的坐标为![]() ;
;
当![]() 时,
时,
同理可得:点P的坐标为![]() ,
,
故点P的坐标为![]() 或
或![]() ;
;
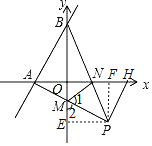
![]() 过点P作
过点P作![]() 交x轴于H,过点P分别作x、y轴的垂线,交于点F、E,
交x轴于H,过点P分别作x、y轴的垂线,交于点F、E,
由![]() 知,
知,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,又
,又![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
又![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() .
.
故答案为:(1)-2, 4;(2)①(4, 0);②(2,-2)或(4,2);(3)见解析.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目