题目内容
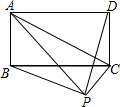已知矩形ABCD，当点P在图中的位置时，则有结论
- A.S△PBC=S△PAC+S△PCD
- B.S△PBC=S△PAC-S△PCD
- C.S△PAB+S△PCD＞
S矩形ABCD - D.S△PAB+S△PCD＜S矩形ABCD
B
分析：过点P作PE⊥AD于E，交BC于F，根据矩形的对边相等可得AD=BC，根据矩形的性质求出S△PAB+S△PCD=S矩形ABCD，再利用S△PAD-S△PBC列式整理即可得解．
解答：
解：如图，过点P作PE⊥AD于E，交BC于F，
在矩形ABCD中，AD=BC，
易得S△PAB+S△PCD=S矩形ABCD，故C、D错误；
S△PAD-S△PBC=AD•PE-BC•PF=AD•（PE-PF）=AD•EF=S矩形ABCD=S△ABC=S△PAB+S△PAC-S△PBC，
即S△PAD=S△PAB+S△PAC，
∵S△PAD=S矩形ABCD+S△PBC，
S△PAB=S矩形ABCD-S△PCD，
∴S矩形ABCD+S△PBC=S矩形ABCD-S△PCD+S△PAC，
即S△PBC=S△PAC-S△PCD；故A选项错误，B选项正确．
故选B．
点评：本题考查了矩形的性质，三角形的面积，难度较大，解题关键在于求出S△PAD=S△PAB+S△PAC．
分析：过点P作PE⊥AD于E，交BC于F，根据矩形的对边相等可得AD=BC，根据矩形的性质求出S△PAB+S△PCD=
S矩形ABCD，再利用S△PAD-S△PBC列式整理即可得解．解答：
解：如图，过点P作PE⊥AD于E，交BC于F，在矩形ABCD中，AD=BC，
易得S△PAB+S△PCD=
S矩形ABCD，故C、D错误；S△PAD-S△PBC=
AD•PE-BC•PF=AD•（PE-PF）=AD•EF=S矩形ABCD=S△ABC=S△PAB+S△PAC-S△PBC，即S△PAD=S△PAB+S△PAC，
∵S△PAD=
S矩形ABCD+S△PBC，S△PAB=
S矩形ABCD-S△PCD，∴
S矩形ABCD+S△PBC=S矩形ABCD-S△PCD+S△PAC，即S△PBC=S△PAC-S△PCD；故A选项错误，B选项正确．
故选B．
点评：本题考查了矩形的性质，三角形的面积，难度较大，解题关键在于求出S△PAD=S△PAB+S△PAC．
练习册系列答案
阅读快车系列答案
相关题目
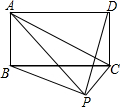已知矩形ABCD，当点P在图中的位置时，则有结论（ ）