Question

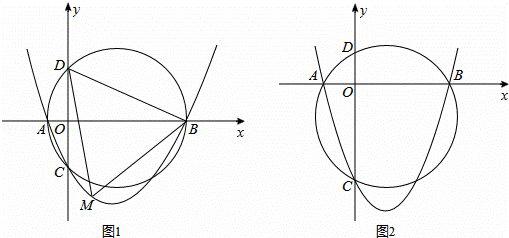
图，已知抛物线y=ax²+bx+c（a＞0，c＜0）交x轴于点A，B，交y轴于点C，设过点A，B，C三点的圆与y轴的另一个交点为D．

（1）如图1，已知点A，B，C的坐标分别为（﹣2，0），（8，0），（0，﹣4）；

①求此抛物线的表达式与点D的坐标；

②若点M为抛物线上的一动点，且位于第四象限，求△BDM面积的最大值；

（2）如图2，若a=1，求证：无论b，c取何值，点D均为顶点，求出该定点坐标．

Answer 1

解：（1）∵抛物线y=ax²+bx+c过点A（﹣2，0），B（8，0），C（0，﹣4），

∴，解得，

∴抛物线的解析式为：y=x²﹣x﹣4；

∵OA=2，OB=8，OC=4，∴AB=10．

如答图1，连接AC、BC．

由勾股定理得：AC=，BC=．

∵AC²+BC²=AB²=100，

∴∠ACB=90°，

∴AB为圆的直径．

由垂径定理可知，点C、D关于直径AB对称，

∴D（0，4）．

 

（2）解法一：

设直线BD的解析式为y=kx+b，∵B（8，0），D（0，4），

∴，解得，

∴直线BD解析式为：y=﹣x+4．

设M（x，x²﹣x﹣4），

如答图2﹣1，过点M作ME∥y轴，交BD于点E，则E（x，﹣x+4）．

∴ME=（﹣x+4）﹣（x²﹣x﹣4）=﹣x²+x+8．

∴S_△BDM=S_△MED+S_△MEB=ME（x_E﹣x_D）+ME（x_B﹣x_D）=ME（x_B﹣x_D）=4ME，

∴S_△BDM=4（﹣x²+x+8）=﹣x²+4x+32=﹣（x﹣2）²+36．

∴当x=2时，△BDM的面积有最大值为36；

解法二：

如答图2﹣2，过M作MN⊥y轴于点N．

设M（m，m²﹣m﹣4），

∵S_△OBD=OB•OD==16，

S_梯形OBMN=（MN+OB）•ON

=（m+8）[﹣（m²﹣m﹣4）]

=﹣m（m²﹣m﹣4）﹣4（m²﹣m﹣4），

S_△MND=MN•DN

=m[4﹣（m²﹣m﹣4）]

=2m﹣m（m²﹣m﹣4），

∴S_△BDM=S_△OBD+S_梯形OBMN﹣S_△MND

=16﹣m（m²﹣m﹣4）﹣4（m²﹣m﹣4）﹣2m+m（m²﹣m﹣4）

=16﹣4（m²﹣m﹣4）﹣2m

=﹣m²+4m+32

=﹣（m﹣2）²+36；

∴当m=2时，△BDM的面积有最大值为36．

 

（3）如答图3，连接AD、BC．

由圆周角定理得：∠ADO=∠CBO，∠DAO=∠BCO，

∴△AOD∽△COB，

∴=，

设A（x₁，0），B（x₂，0），

∵已知抛物线y=x²+bx+c（c＜0），

∵OC=﹣c，x₁x₂=c，

∴=，

∴OD==1，

∴无论b，c取何值，点D均为定点，该定点坐标D（0，1）．