题目内容
如图,在平面直角系中,直线AB:y=| 4 |
| a |
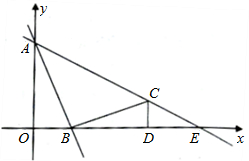 作CD⊥x轴交AE于C.连接BC,当动点B在线段OD上运动(不与点O点D重合)且AB⊥BC时.
作CD⊥x轴交AE于C.连接BC,当动点B在线段OD上运动(不与点O点D重合)且AB⊥BC时.(1)求证:△ABO∽△BCD;
(2)求线段CD的长(用a的代数式表示);
(3)若直线AE的方程是y=-
| 13 |
| 16 |
分析:(1)根据已知得出∠BAO=∠CBD,以及再利用∠CDO=∠AOD=90°,即可得出三角形相似;
(2)利用相似三角形的性质得出
=
,进而表示出CD的长;
(3)根据C点坐标求出a的值,进而求出tan∠BAC=
=
=
的值即可.
(2)利用相似三角形的性质得出
| CD |
| OB |
| BD |
| AO |
(3)根据C点坐标求出a的值,进而求出tan∠BAC=
| BC |
| AB |
| BD |
| AO |
| 4+a |
| 4 |
解答:(1)证明:∵CD⊥BE,
∴∠CDO=∠AOD=90°,
∴∠ABO+∠BAO=90°,
∵CB⊥AB,∴∠ABO+∠CBD=90°,
∴∠BAO=∠CBD,
∴△ABO∽△BCD;
(2)解:∵A(0,4),B(-a,0)(a<0),
∴AO=4,BO=-a,
∵△ABO∽△BCD,
∴
=
,
∵OD=AO=4,
∴CD=
(-4<a<0),
(3)解:∵C(4,
),
b=4,
∴
=-
×4+4,
即:a2+4a+3=0,
解得:a1=-1,a2=-3,
∵△ABO∽△BCD,
∴
=
,
在Rt△ABC中,∠ABC=90°,
tan∠BAC=
=
=
,
当a1=-1时,tan∠BAC=
,
当a2=-3时,tan∠BAC=
.
综上所述:tan∠BAC=
或tan∠BAC=
.
∴∠CDO=∠AOD=90°,
∴∠ABO+∠BAO=90°,
∵CB⊥AB,∴∠ABO+∠CBD=90°,
∴∠BAO=∠CBD,
∴△ABO∽△BCD;
(2)解:∵A(0,4),B(-a,0)(a<0),
∴AO=4,BO=-a,
∵△ABO∽△BCD,
∴
| CD |
| OB |
| BD |
| AO |

∵OD=AO=4,
∴CD=
| -a(4+a) |
| 4 |
(3)解:∵C(4,
| -a(4+a) |
| 4 |
b=4,
∴
| -a(4+a) |
| 4 |
| 13 |
| 16 |
即:a2+4a+3=0,
解得:a1=-1,a2=-3,
∵△ABO∽△BCD,
∴
| BC |
| AB |
| BD |
| AO |
在Rt△ABC中,∠ABC=90°,
tan∠BAC=
| BC |
| AB |
| BD |
| AO |
| 4+a |
| 4 |
当a1=-1时,tan∠BAC=
| 3 |
| 4 |
当a2=-3时,tan∠BAC=
| 1 |
| 4 |
综上所述:tan∠BAC=
| 3 |
| 4 |
| 1 |
| 4 |
点评:此题主要考查了一次函数的综合应用以及相似三角形的判定与性质,灵活利用相似三角形的性质是解题关键.

练习册系列答案
相关题目
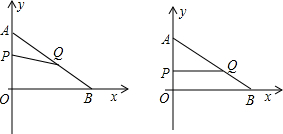
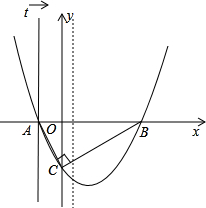 y轴的负半轴上,且∠ACB=90°
y轴的负半轴上,且∠ACB=90°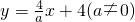 分别交x轴、y轴于B、A两点.直线AE分别交x轴、y轴于E、A两点,D是x轴上的一点,OA=OD.过D
分别交x轴、y轴于B、A两点.直线AE分别交x轴、y轴于E、A两点,D是x轴上的一点,OA=OD.过D 作CD⊥x轴交AE于C.连接BC,当动点B在线段OD上运动(不与点O点D重合)且AB⊥BC时.
作CD⊥x轴交AE于C.连接BC,当动点B在线段OD上运动(不与点O点D重合)且AB⊥BC时.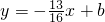 ,求tan∠BAC的值.
,求tan∠BAC的值.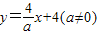 分别交x轴、y轴于B、A两点.直线AE分别交x轴、y轴于E、A两点,D是x轴上的一点,OA=OD.过D作CD⊥x轴交AE于C.连接BC,当动点B在线段OD上运动(不与点O点D重合)且AB⊥BC时.
分别交x轴、y轴于B、A两点.直线AE分别交x轴、y轴于E、A两点,D是x轴上的一点,OA=OD.过D作CD⊥x轴交AE于C.连接BC,当动点B在线段OD上运动(不与点O点D重合)且AB⊥BC时.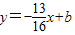 ,求tan∠BAC的值.
,求tan∠BAC的值.