Question

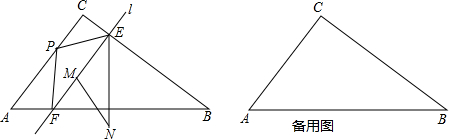
（2013•玄武区二模）在梯形ABCD中，AD∥BC，∠D=90°，以AB为直径作⊙O．
（1）如图①，⊙O与DC相切于点E，试说明：∠BAE=∠DAE；
（2）如图②，⊙O与DC交于点E、F．
①哪一个角与∠BAE相等？为什么？
②试探究线段DF与CE的数量关系．

Answer 1

分析：（1）根据切线的性质得出AD∥OE，利用等角对等边以及平行线的性质得出∠BAE=∠DAE；
（2）①利用圆内接四边形的性质以及圆周角定理得出∠ABE+∠BAE=90°，∠DAF+∠AFD=90°，由∠ABE=∠AFD，得出∠DAF=∠BAE；
②首先得出四边形ANCD是矩形，进而得出△DAF≌△CNE，即可得出答案．

解答：（1）证明：连接OE，
∵⊙O与DC相切于点E，
∴OE⊥CD，
∵∠D=90°，
∴AD∥OE，
∴∠DAE=∠AEO，
∵OA=OE，
∴∠OAE=∠OEA，
∴∠BAE=∠DAE；

（2）解：①∠DAF与∠BAE相等，理由如下：
连接BE，
∵AB为直径作⊙O，
∴∠BEA=90°，
∴∠ABE+∠BAE=90°，
∵四边形ABEF是⊙O的圆内接四边形，
∴∠ABE=∠AFD，
又∵∠DAF+∠AFD=90°，
∴∠DAF=∠BAE，
②DF=CE，理由如下：
连接AN，NE，
∵AB为直径作⊙O，
∴∠BNA=90°，
∵AD∥BC，∠D=90°，
∴∠D=∠ANC=∠C=90°，
∴四边形ANCD是矩形，
∴AD=NC，
∴∠ENC=∠BAE，
∵∠DAF=∠BAE，
∴∠DAF=∠ENC，
在△DAF和△CNE中，

∠D=∠C DA=NC ∠DAF=∠CNE

，
∴△DAF≌△CNE（ASA），
∴DF=EC．

点评：此题主要考查了圆的综合应用以及圆周角定理和全等三角形的判定以及矩形的性质和判定等知识，熟练利用圆周角定理得出∠BAE=∠DAE是解题关键．