��Ŀ����
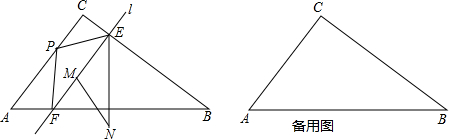
��2013•��������ģ����ͼ����Rt��ABC�У���C=90�㣬AC=6��BC=8������P�ӵ�A��ʼ������AC-CB-BA�˶�����P��AC��CB��BA�����˶����ٶȷֱ�Ϊÿ��3��4��5����λ��ֱ��l����AC�غϵ�λ�ÿ�ʼ����ÿ��
����λ���ٶ���CB����ƽ���ƶ������ƶ������б���l��AC���ҷֱ���CB��AB�߽���E��F���㣬��P��ֱ��lͬʱ���������˶���ʱ��Ϊt�룬����P��һ�λص���Aʱ����P��ֱ��lͬʱֹͣ�˶���
��1����t=5��ʱ����P�߹���·����Ϊ
��2������P��AC�����˶�ʱ������PEF�Ƶ�E��ʱ����ת��ʹ�õ�P�Ķ�Ӧ��M����EF�ϣ���F�Ķ�Ӧ���Ϊ��N����EN��ABʱ����t��ֵ��
��3������P������AC-CB-BA���˶�ʱ������P����ֱ��EF�ĶԳƵ㣬��Ϊ��Q���ڵ�P��ֱ��l�˶��Ĺ����У����γɵ��ı���PEQFΪ���Σ���ֱ��д��t��ֵ��
| 4 | 3 |
��1����t=5��ʱ����P�߹���·����Ϊ
19
19
����t=3
3
��ʱ����P���E�غϣ���2������P��AC�����˶�ʱ������PEF�Ƶ�E��ʱ����ת��ʹ�õ�P�Ķ�Ӧ��M����EF�ϣ���F�Ķ�Ӧ���Ϊ��N����EN��ABʱ����t��ֵ��
��3������P������AC-CB-BA���˶�ʱ������P����ֱ��EF�ĶԳƵ㣬��Ϊ��Q���ڵ�P��ֱ��l�˶��Ĺ����У����γɵ��ı���PEQFΪ���Σ���ֱ��д��t��ֵ��

��������1���������������AB=10������P���ڸ��ߵ��ٶȿ�������ڸ������õ�ʱ�䣬�Ӷ��������P��5�����ߵ�·�̣�����CE=P�ߵ�·��-AC�������̾Ϳ��������ֵ��
��2����ͼ���ɵ�P�Ķ�Ӧ��M����EF�ϣ���F�Ķ�Ӧ��Ϊ��N����֪��PEF=��MEN����EF��AC����C=90����Եó���CPE=��PEF������EN��AB�����С�B=��MEN�����Եó���CPE=��B������������Ǻ����Ĺ�ϵ��������������Ϳ����ˣ�
��3���������ε����ʺ����������ε����ʷ����������P����AC��ʱ�͵�P��AB��ʱ���Էֱ����t��ֵ��
��2����ͼ���ɵ�P�Ķ�Ӧ��M����EF�ϣ���F�Ķ�Ӧ��Ϊ��N����֪��PEF=��MEN����EF��AC����C=90����Եó���CPE=��PEF������EN��AB�����С�B=��MEN�����Եó���CPE=��B������������Ǻ����Ĺ�ϵ��������������Ϳ����ˣ�
��3���������ε����ʺ����������ε����ʷ����������P����AC��ʱ�͵�P��AB��ʱ���Էֱ����t��ֵ��
����⣺��1����Rt��ABC�У���C=90�㣬AC=6��BC=8��
�ɹ��ɶ�������AB=10��
�ߵ�P��AC��CB��BA�����˶����ٶȷֱ�Ϊÿ��3��4��5����λ��
���P��AC�����˶���ʱ��Ϊ��6��3=2�룬
��P��BC�����˶���ʱ��Ϊ��8��4=2�룬
���P��AB�����˶���ʱ��Ϊ��5-2-2=1�룬
��P����AB�����˶��ľ���Ϊ��5��1=5��
�൱t=5��ʱ����P�߹���·����Ϊ 19��
�������֪������t-2����4=
tʱ����P���E�غϣ�
��ã�t=3��
��t=3��ʱ����P���E�غϣ�
�ʴ�Ϊ��19��3��
��2����ͼ���ɵ�P�Ķ�Ӧ��M����EF�ϣ���F�Ķ�Ӧ��Ϊ��N����֪��PEF=��MEN��
��P��AC�ϣ�
��AP=3t ��0��t��2����
��CP=6-3t��CE=
t��
��EF��AC����C=90�㣬
���BEF=90�㣬��CPE=��PEF��
��EN��AB��
���B=��MEN��
�ߡ�PEF=��FEN��
���CPE=��B��
��tan��CPE=
��tanB=
=
��
��CP=
CE��
��CP=
��
t=
t
��6-3t=
t��
��ã�t=
��
��3����ͼ1����P����AC��ʱ����0��t��2��
��AP=3t��PC=6-3t��EC=
t��
��BE=8-
t��
��EF��AC��
���FEB�ס�ACB��
��
=
��
��
=
��
��EF=6-t��
���ı���PEQF�����Σ�
���POE=90�㣬OE=
EF=3-
t��
��EF��AC����C=90�㣬
���OEC=90�㣬
���ı���PCEO�Ǿ��Σ�
��OE=PC��
��3-
t=6-3t��
��t=
��
��ͼ2����P��AB��ʱ��4��t��6����
���ı���PFQE�����Σ�
��PE=PF��
���PFE=��PEF��
��EF��AC����C=90�㣬
���FEB=��FEP+��PEB=90�㣬
���B+��EFB=90�㣬
���B+��FEP=90�㣬
���PEB=��B��
��PE=PB��
��PB=5��t-4����
��BF=10��t-4����
��sin��B=
=
��
��
=
��
��EF=6t-24
��CE=
t��
��BE=8-
t��
�ߡ�FEB�ס�ACB��
��
=
��
��
=
��
��EF=6-t��
��6-t=6t-24
���t=
��t��ֵΪ
���룩��
���룩��
�ɹ��ɶ�������AB=10��
�ߵ�P��AC��CB��BA�����˶����ٶȷֱ�Ϊÿ��3��4��5����λ��
���P��AC�����˶���ʱ��Ϊ��6��3=2�룬
��P��BC�����˶���ʱ��Ϊ��8��4=2�룬
���P��AB�����˶���ʱ��Ϊ��5-2-2=1�룬
��P����AB�����˶��ľ���Ϊ��5��1=5��
�൱t=5��ʱ����P�߹���·����Ϊ 19��
�������֪������t-2����4=
| 4 |
| 3 |
��ã�t=3��
��t=3��ʱ����P���E�غϣ�
�ʴ�Ϊ��19��3��
��2����ͼ���ɵ�P�Ķ�Ӧ��M����EF�ϣ���F�Ķ�Ӧ��Ϊ��N����֪��PEF=��MEN��
��P��AC�ϣ�
��AP=3t ��0��t��2����
��CP=6-3t��CE=
| 4 |
| 3 |
��EF��AC����C=90�㣬
���BEF=90�㣬��CPE=��PEF��
��EN��AB��
���B=��MEN��
�ߡ�PEF=��FEN��
���CPE=��B��
��tan��CPE=
| CE |
| CP |
| AC |
| BC |
| 3 |
| 4 |
��CP=
| 4 |
| 3 |
��CP=
| 4 |
| 3 |
| 4 |
| 3 |
| 16 |
| 9 |
��6-3t=
| 16 |
| 9 |
��ã�t=
| 54 |
| 43 |
��3����ͼ1����P����AC��ʱ����0��t��2��
��AP=3t��PC=6-3t��EC=
| 4 |
| 3 |
��BE=8-
| 4 |
| 3 |
��EF��AC��
���FEB�ס�ACB��
��
| EF |
| AC |
| BE |
| BC |
��
| EF |
| 6 |
8-
| ||
| 8 |
��EF=6-t��
���ı���PEQF�����Σ�
���POE=90�㣬OE=
| 1 |
| 2 |
| 1 |
| 2 |
��EF��AC����C=90�㣬
���OEC=90�㣬
���ı���PCEO�Ǿ��Σ�
��OE=PC��
��3-
| 1 |
| 2 |
��t=
| 6 |
| 5 |

��ͼ2����P��AB��ʱ��4��t��6����
���ı���PFQE�����Σ�
��PE=PF��
���PFE=��PEF��
��EF��AC����C=90�㣬
���FEB=��FEP+��PEB=90�㣬
���B+��EFB=90�㣬
���B+��FEP=90�㣬
���PEB=��B��
��PE=PB��
��PB=5��t-4����
��BF=10��t-4����
��sin��B=
| 3 |
| 5 |
| EF |
| BF |
��
| EF |
| 10(t-4) |
| 3 |
| 5 |
��EF=6t-24
��CE=
| 4 |
| 3 |
��BE=8-
| 4 |
| 3 |
�ߡ�FEB�ס�ACB��
��
| EF |
| AC |
| BE |
| BC |
��
| EF |
| 6 |
8-
| ||
| 8 |
��EF=6-t��
��6-t=6t-24
���t=
| 30 |
| 7 |
��t��ֵΪ
| 6 |
| 5 |
| 30 |
| 7 |
���������⿼���˹��ɶ��������ã����������ε��ж������ʵ����ã����ε����ʵ����ã����Ǻ���ֵ�����ü���������˼������ã������ʱ�������������ε����ʺ����ε������ǹؼ���

��ϰ��ϵ�д�
 ������������ϵ�д�
������������ϵ�д�
�����Ŀ