题目内容
如图所示，根据提供的数据回答下列问题．
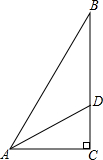
（1）在图①中，sinA=______，cosA=______，sin2A+cos2A=______；
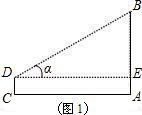
在图②中，sinA1=______，cosA1=______，sin2A1+cos2A1=______；
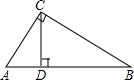
在图③中，sinA2=______，cosA2=______，sin2A2+cos2A2=______．
通过以上三个特殊例子，你发现了什么规律？用一个一般式子把你发现的规律表示出来并加以证明．
（2）在图①中，tanA=______，
=______；
在图②中，tanA1=______，
=______；
在图③中，tanA2=______，
=______．
通过以上三个特殊例子，你发现了什么规律？用一个一般式子表示你发现的规律并加以证明．
（1）在图①中，sinA=______，cosA=______，sin2A+cos2A=______；
在图②中，sinA1=______，cosA1=______，sin2A1+cos2A1=______；
在图③中，sinA2=______，cosA2=______，sin2A2+cos2A2=______．
通过以上三个特殊例子，你发现了什么规律？用一个一般式子把你发现的规律表示出来并加以证明．
（2）在图①中，tanA=______，
| sinA |
| cosA |
在图②中，tanA1=______，
| sinA1 |
| cosA1 |
在图③中，tanA2=______，
| sinA2 |
| cosA2 |
通过以上三个特殊例子，你发现了什么规律？用一个一般式子表示你发现的规律并加以证明．
sin2A+cos2A=1，tanA=
，
证明：∵如图①，sinA=
，cosA=
，tanA=
，
∴sin2A+cos2A=（
）2+（
）2
=
+
=
=
=1，
即sin2A+cos2A=1；
=
=
，
∵tanA=
，
∴tanA=
即sin2A+cos2A=1；
故答案为：
，
，1，
，
，1，
，
，
，
，
，
．
| sinA |
| cosA |
证明：∵如图①，sinA=
| BC |
| AB |
| AC |
| AB |
| BC |
| AC |
∴sin2A+cos2A=（
| BC |
| AB |
| AC |
| AB |
=
| BC2 |
| AB2 |
| AC2 |
| AB2 |
=
| BC2+AC2 |
| AB2 |
=
| AB2 |
| AB2 |
=1，
即sin2A+cos2A=1；
| sinA |
| cosA |
| ||
|
| BC |
| AC |
∵tanA=
| BC |
| AC |
∴tanA=
| sinA |
| cosA |
即sin2A+cos2A=1；
故答案为：
| 4 |
| 5 |
| 3 |
| 5 |
| 12 |
| 13 |
| 5 |
| 13 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 12 |
| 5 |
| 12 |
| 5 |
练习册系列答案
一线名师权威作业本系列答案
相关题目
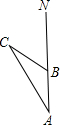的速度前行2h到达B处，此时GPS显示村庄C在北偏西60°方向．
