��Ŀ����
����ͼ����·������CF��DE����ƽ�У��߶�CDΪ���к������·�����A��B����ֱ��ʾ��վ�ͳ��У�CD��AB����ֱ����ƽ�У��Ҷ�����·�����ߴ�ֱ����·��20�ף�A��B���62�ף���A=67�㣬��B=37�㣮
��1����CD��AB֮��ľ��룻
��2��ij�˴ӳ�վA������������A��D��C��Bȥ����B������������A��D��C��B���ﳬ�б�ֱ�Ӻᴩ��·���߶����ף�
���ο����ݣ�sin67���
 ��cos67���
��cos67���
 ��tan67���
��tan67���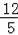
 ��sin37���
��sin37���
 ��cos37���
��cos37���
 ��tan37���
��tan37���
 ��
��


�����㡿��ֱ�������ε�Ӧ�ã�
����������1����CD��AB֮��ľ���Ϊx������Rt��BCF��Rt��ADE�зֱ���x��ʾBF��AE����AB=AE+EF+FB�����뼴�����x��ֵ��
��2����Rt��BCF��Rt��ADE�У��ֱ����BC��AD�ij��ȣ����AD+DC+CB��AB��ֵ������⣮
����𡿽⣺��1��CD��AB֮��ľ���Ϊx��
����Rt��BCF��Rt��ADE��
��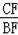
 =tan37�㣬
=tan37�㣬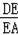
 =tan67�㣬
=tan67�㣬
��BF=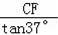
 ��
��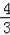
 x��AE=
x��AE=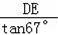
 ��
��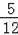
 x��
x��
�֡�AB=62��CD=20��
��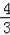
 x+
x+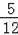
 x+20=62��
x+20=62��
��ã�x=24��
��CD��AB֮��ľ���ԼΪ24�ף�
��2����Rt��BCF��Rt��ADE��
��BC=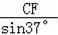
 ��
��
 =40��
=40��
AD=
 ��
��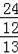
 =26��
=26��
��AD+DC+CB��AB=40+20+26��62=24���ף���
����������A��D��C��B���ﳬ�б�ֱ�Ӻᴩ��·����Լ24�ף�


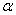 ��б����ʻ500�ף����������ĸ߶���( )
��б����ʻ500�ף����������ĸ߶���( ) �� B.
�� B. �� C.
�� C. �� D.
�� D.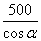 ��
�� 



 ��2sin45�㩁��
��2sin45�㩁��


 ��
�� �������50ǧ�ף�����ij������1ʱ�����г���
�������50ǧ�ף�����ij������1ʱ�����г��� ���߶�
���߶� �ֱ��ʾ�ס�������ʻ��·��
�ֱ��ʾ�ס�������ʻ��·�� ��ǧ�ף����������ʱ��
��ǧ�ף����������ʱ�� ��ʱ��֮��Ĺ�ϵ������ͼ��ش��������⣺
��ʱ��֮��Ĺ�ϵ������ͼ��ش��������⣺