题目内容
如图，C为弧AB的中点，CN⊥OB于N，CD⊥OA于M，CN=4cm，则CD=________cm．
8
分析：根据圆心角、弧、弦之间关系求出∠AOC=∠BOC，根据角平分线性质得出CM=CN=4cm，根据垂径定理得出CD=2CM，代入求出即可．
解答：
连接OC，
∵C为弧AB的中点，
∴弧AC=弧BC，
∴∠AOC=∠BOC，
∵CN⊥OB，CD⊥OA，CN=4cm，
∴CM=CN=4cm，
∵CM⊥OA，
即OM⊥CD，
由垂径定理得：CD=2CM=8cm，
故答案为：8．
点评：本题考查了圆心角、弧、弦之间关系、垂径定理，角平分线性质等知识点，关键是求出CM的长和得出CD=2CM．
分析：根据圆心角、弧、弦之间关系求出∠AOC=∠BOC，根据角平分线性质得出CM=CN=4cm，根据垂径定理得出CD=2CM，代入求出即可．
解答：
连接OC，∵C为弧AB的中点，
∴弧AC=弧BC，
∴∠AOC=∠BOC，
∵CN⊥OB，CD⊥OA，CN=4cm，
∴CM=CN=4cm，
∵CM⊥OA，
即OM⊥CD，
由垂径定理得：CD=2CM=8cm，
故答案为：8．
点评：本题考查了圆心角、弧、弦之间关系、垂径定理，角平分线性质等知识点，关键是求出CM的长和得出CD=2CM．
练习册系列答案
相关题目
如图，在半径为1的⊙O中，AB为直径，C为弧AB的中点，D为弧CB的三等分点，且弧DB的长等于弧CD长的两倍，连接AD并延长交⊙O的切线CE于点E（C为切点），则AE的长为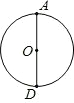
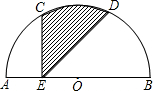如图所示，AB为半圆的直径，C、D为弧
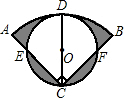如图，扇形CAB的圆心角∠ACB=90°，半径CA=8cm，D为弧AB的中点，以CD为直径的⊙O与CA、CB相交于点E、F，则图中阴影部分的面积是
如图，在⊙O中D为弧AB的中点，CD为直径，弦AB交CD于P，PE⊥BC于E，BC=12，CE：EB=3：1，求AB的长．