Question

如图，BC是⊙O的直径，AC切⊙O于点C，AB交⊙O于点D，若AD：DB=2：3，AC=10，则sinB=________．

Answer 1

分析：连接CD，根据圆周角定理可知CD⊥AB；在Rt△ABC中，CD⊥AB，可用未知数设出AD、BD的长，进而由射影定理求得AD的值；易知∠ACD=∠B，在Rt△ACD中，可根据AD、AC的长，求出∠ACD的正弦值，由此得解．
解答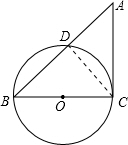：解：连接CD，则CD⊥AB；
∵AC切⊙O于C，
∴AC⊥BC；
在Rt△ACB中，CD⊥AB，则有：
AC²=AD•AB；
设AD=2k，BD=3k，则AB=5k；
∴10²=2k•5k，解得k=，
∴AD=2k=2，
∴sinB=sin∠ACD==．
点评：此题中主要考查了切线的性质以及圆周角定理的应用．