题目内容
 如图所示,△ABC在平面直角坐标系中,将△ABC向右平移5个单位得到△A1B1C1,再将△A1B1C1绕点B1顺时针旋转90°得到△A2B2C2.
如图所示,△ABC在平面直角坐标系中,将△ABC向右平移5个单位得到△A1B1C1,再将△A1B1C1绕点B1顺时针旋转90°得到△A2B2C2.
(1)作出△A1B1C1和△A2B2C2;
(2)直接写出△A1B1C1旋转时绕过的面积.
 解:(1)△A1B1C1和△A2B2C2如图所示;
解:(1)△A1B1C1和△A2B2C2如图所示;(2)根据勾股定理,A1B1=
 =5,
=5,△A1B1C1旋转时绕过的面积=扇形A1B1A2的面积+△A2B2C2的面积,
=
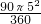 +
+ ×2×3,
×2×3,=
 π+3.
π+3.分析:(1)根据网格结构分别找出平移后的对应点A1、B1、C1的位置和旋转后的对应点A2、B2、C2的位置,然后顺次连接即可;
(2)利用勾股定理列式求出A1B1的长,再根据△A1B1C1旋转时绕过的面积=扇形A1B1A2的面积+△A2B2C2的面积,然后列式进行计算即可得解.
点评:本题考查了利用旋转变换作图,扇形的面积计算,熟练掌握网格结构,准确找出对应点的位置是解题的关键.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
 如图所示,△ABC在坐标平面内三个顶点的坐标分别为A(0,-2),B(3,-1),C(2,1).
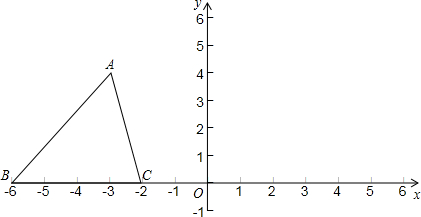
如图所示,△ABC在坐标平面内三个顶点的坐标分别为A(0,-2),B(3,-1),C(2,1). 如图所示,△ABC在正方形网格中,若点A的坐标为(0,4),按要求回答下列问题:
如图所示,△ABC在正方形网格中,若点A的坐标为(0,4),按要求回答下列问题: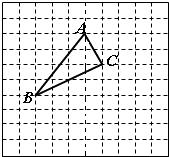 如图所示,△ABC在正方形网格中,若点A的坐标为(0,5),按要求回答下列问题:
如图所示,△ABC在正方形网格中,若点A的坐标为(0,5),按要求回答下列问题: 如图所示,△ABC在正方形网格中,若点A的坐标为(0,3),按要求回答下列问题:
如图所示,△ABC在正方形网格中,若点A的坐标为(0,3),按要求回答下列问题: