题目内容
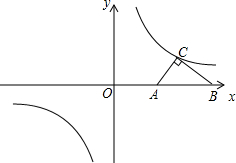 Rt△ABC中,∠C=90°,AB=5,BC=4,将它放在直角坐标系中,使斜边AB在x轴上,直角顶点C在反比例函数y=
Rt△ABC中,∠C=90°,AB=5,BC=4,将它放在直角坐标系中,使斜边AB在x轴上,直角顶点C在反比例函数y=| 12 | x |
(1)当Rt△ABC按如图所示放置,求出点A的坐标.
(2)如果改变Rt△ABC的放置方式,A点的坐标还可能是
(6.8,0),(-3.2,0),(-6.8,0)
(6.8,0),(-3.2,0),(-6.8,0)
.分析:(1)作CM⊥AB于点M,利用勾股定理得出AC的长,进而得出CM的长,再利用反比例函数图象上点的坐标性质得出C点坐标,进而得出AM的长,即可得出A点坐标;
(2)利用改变Rt△ABC的放置方式,结合图形以及(1)中所求得出所有符合条件的点即可.
(2)利用改变Rt△ABC的放置方式,结合图形以及(1)中所求得出所有符合条件的点即可.
解答: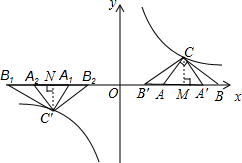 解:(1)如图所示:作CM⊥AB于点M,
解:(1)如图所示:作CM⊥AB于点M,
∵Rt△ABC中,∠C=90°,AB=5,BC=4,
∴AC=
=3,
∴
×AC×BC=
×CM×AB,
∴
×3×4=
×CM×5
解得:CM=2.4,
在y=
中,当y=2.4时,x=5,
∴C(5,2.4),
在Rt△ACM中,
AM=
=1.8,
∴OA=5-1.8=3.2,
即A(3.2,0);
(2)如图所示:过点C′作C′N⊥y轴于点N,
由(1)可得出C′N=CM=2.4,
A1N=A2N=AM=A′M=1.8,NO=MO=5,
∴A′O=5+1.8=6.8,
∴A′点坐标为:(6.8,0),
∴A1O=5-1.8=3.2,
∴A1点坐标为:(-3.2,0),
∴A2O=5+1.8=6.8,
∴A2点坐标为:(-6.8,0),
综上所述:A点的坐标还可能是(6.8,0),(-3.2,0),(-6.8,0).
故答案为:(6.8,0),(-3.2,0),(-6.8,0).
 解:(1)如图所示:作CM⊥AB于点M,
解:(1)如图所示:作CM⊥AB于点M,∵Rt△ABC中,∠C=90°,AB=5,BC=4,
∴AC=
| 52-42 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
解得:CM=2.4,
在y=
| 12 |
| x |
∴C(5,2.4),
在Rt△ACM中,
AM=
| 32-2.42 |
∴OA=5-1.8=3.2,
即A(3.2,0);
(2)如图所示:过点C′作C′N⊥y轴于点N,
由(1)可得出C′N=CM=2.4,
A1N=A2N=AM=A′M=1.8,NO=MO=5,
∴A′O=5+1.8=6.8,
∴A′点坐标为:(6.8,0),
∴A1O=5-1.8=3.2,
∴A1点坐标为:(-3.2,0),
∴A2O=5+1.8=6.8,
∴A2点坐标为:(-6.8,0),
综上所述:A点的坐标还可能是(6.8,0),(-3.2,0),(-6.8,0).
故答案为:(6.8,0),(-3.2,0),(-6.8,0).
点评:此题主要考查了反比例函数的综合应用以及勾股定理的应用,根据数形结合得出所有符合条件的点是解题关键.

练习册系列答案
相关题目
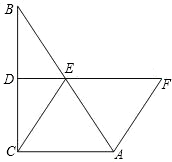 延长线上,且AF=CE.求证:四边形ACEF是菱形.
延长线上,且AF=CE.求证:四边形ACEF是菱形. 如图,在Rt△ABC中,∠BAC=90°,点D、E、F分别是三边的中点,且CF=3cm,则DE=
如图,在Rt△ABC中,∠BAC=90°,点D、E、F分别是三边的中点,且CF=3cm,则DE=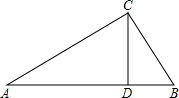 如图,Rt△ABC中,AC⊥BC,CD⊥AB于D,AC=8,BC=6,则AD=
如图,Rt△ABC中,AC⊥BC,CD⊥AB于D,AC=8,BC=6,则AD=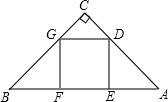 点G在边BC上.
点G在边BC上. 如图,Rt△ABC中,∠C=90°,D为AB的中点,DE⊥AB,AB=20,AC=12,则四边形ADEC的面积为
如图,Rt△ABC中,∠C=90°,D为AB的中点,DE⊥AB,AB=20,AC=12,则四边形ADEC的面积为