题目内容
如图所示，棋盘上有A、B、C三个黑子与P、Q两个白子，要使△ABC∽△RPQ，则第三个白子R应放的位置可以是________．（答案填：“甲、乙、丙、丁”）
丁
分析：应用两三角形相似的判定定理，结合图形分析即可得出结果．
解答：由图可知BC=2，AB=BC=
=
，P，Q=4，
所以PQ：BC=4：2=2．
而与AC=比为2的数是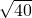 
，
在甲乙丙丁四点中，只有点丁与P、Q连线是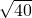，所以选择丁．
故答案为丁．
点评：本题考查了相似三角形的判定，有一定难度，考查三角形相似的判定，注意小方格作用．
分析：应用两三角形相似的判定定理，结合图形分析即可得出结果．
解答：由图可知BC=2，AB=BC=
=，P，Q=4，所以PQ：BC=4：2=2．
而与AC=
比为2的数是 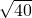，在甲乙丙丁四点中，只有点丁与P、Q连线是
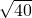，所以选择丁．故答案为丁．
点评：本题考查了相似三角形的判定，有一定难度，考查三角形相似的判定，注意小方格作用．
练习册系列答案
相关题目
如图所示，棋盘上有A、B、C三个黑子与P、Q两个白子，要使△ABC∽△RPQ，则第三个白子R应放的位置可以是（ ）
如图所示，棋盘上有A、B、C三个黑子与P、Q两个白子，要使△ABC∽△RPQ，则第三个白子R应放的位置可以是
