Question

如图，一艘海轮在A点时测得灯塔C在它的北偏东42°方向上，它沿正东方向航行80海里后到达B处，此时灯塔C在它的北偏西55°方向上．

（1）求海轮在航行过程中与灯塔C的最短距离（结果精确到0.1）；

（2）求海轮在B处时与灯塔C的距离（结果保留整数）．

（参考数据：sin55°≈0.819，cos55°≈0.574，tan55°≈1.428，tan42°≈0.900，tan35°≈0.700，tan48°≈1.111）

Answer 1

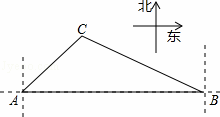
解：（1）C作AB的垂线，设垂足为D，

根据题意可得：∠1=∠2=42°，∠3=∠4=55°，

设CD的长为x海里，

在Rt△ACD中，tan42°=，则AD=x•tan42°，

在Rt△BCD中，tan55°=，则BD=x•tan55°，

∵AB=80，

∴AD+BD=80，

∴x•tan42°+x•tan55°=80，

解得：x≈34.4，

答：海轮在航行过程中与灯塔C的最短距离是34.4海里；

（2）在Rt△BCD中，cos55°=，

∴BC=≈60海里，

答：海轮在B处时与灯塔C的距离是60海里．