题目内容
如图,抛物线y=ax2+bx﹣ 经过点A(1,0)和点B(5,0),与y轴交于点C.
经过点A(1,0)和点B(5,0),与y轴交于点C.
(1)求此抛物线的解析式;
(2)以点A为圆心,作与直线BC相切的⊙A,求⊙A的半径;
(3)在直线BC上方的抛物线上任取一点P,连接PB,PC,请问:△PBC的面积是否存在最大值?若存在,求出这个最大值的此时点P的坐标;若不存在,请说明理由.

解答: 解:(1)∵抛物线y=ax2+bx﹣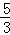 经过点A(1,0)和点B(5,0),
经过点A(1,0)和点B(5,0),
∴把A、B两点坐标代入可得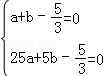 ,解得
,解得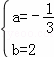 ,
,
∴抛物线解析式为y=﹣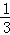 x2+2x﹣
x2+2x﹣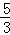 ;
;
(2)过A作AD⊥BC于点D,如图1,
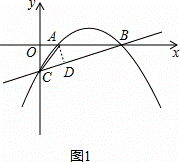
∵⊙A与BC相切,
∴AD为⊙A的半径,
由(1)可知C(0,﹣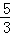 ),且A(1,0),B(5,0),
),且A(1,0),B(5,0),
∴OB=5,AB=OB﹣OA=4,OC=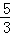 ,
,
在Rt△OBC中,由勾股定理可得BC=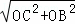 =
=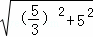 =
=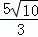 ,
,
∵∠ADB=∠BOC=90°,∠ABD=∠CBO,
∴△ABD∽△CBO,
∴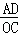 =
=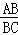 ,即
,即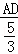 =
=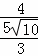 ,解得AD=
,解得AD=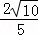 ,
,
即⊙A的半径为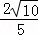 ;
;
(3)∵C(0,﹣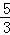 ),
),
∴可设直线BC解析式为y=kx﹣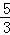 ,
,
把B点坐标代入可求得k=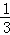 ,
,
∴直线BC的解析式为y=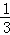 x﹣
x﹣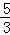 ,
,
过P作PQ∥y轴,交直线BC于点Q,交x轴于点E,如图2,
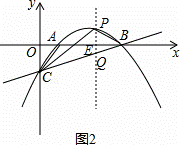
设P(x,﹣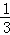 x2+2x﹣
x2+2x﹣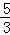 ),则Q(x,
),则Q(x,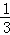 x﹣
x﹣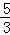 ),
),
∴PQ=(﹣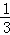 x2+2x﹣
x2+2x﹣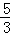 )﹣(
)﹣(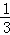 x﹣
x﹣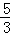 )=﹣
)=﹣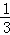 x2+
x2+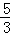 x=﹣
x=﹣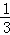 (x﹣
(x﹣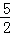 )2+
)2+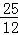 ,
,
∴S△PBC=S△PCQ+S△PBQ= PQ•OE+
PQ•OE+ PQ•BE=
PQ•BE= PQ(OE+BE)=
PQ(OE+BE)= PQ•OB=
PQ•OB=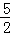 PQ=﹣
PQ=﹣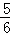 (x﹣
(x﹣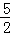 )2+
)2+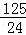 ,
,
∴当x=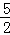 时,S△P
时,S△P BC有最大值
BC有最大值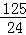 ,此时P点坐标为(
,此时P点坐标为(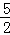 ,
, ),
),
∴当P点坐标为(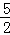 ,
, )时,△PBC的面积有最大值.
)时,△PBC的面积有最大值.

如图是一个正方体展开图,把展开图折叠成正方体后,“我”字一面的相对面上的字是( )

|
| A. | 的 | B. | 中 | C. | 国 | D. | 梦 |
下列图形是将正三角形按一定规律排列,则第4个图形中所有正三角形的个数有( )

|
| A. | 160 | B. | 161 | C. | 162 | D. | 163 |
 D.
D. 
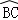 的长l.
的长l.

 B.
B. C.
C. D.
D.
 ﹣3)0+2sin30°﹣
﹣3)0+2sin30°﹣ +|﹣2|.
+|﹣2|.